Concepts Used
DFS , Recursion
Difficulty Level
Medium
Problem Statement :
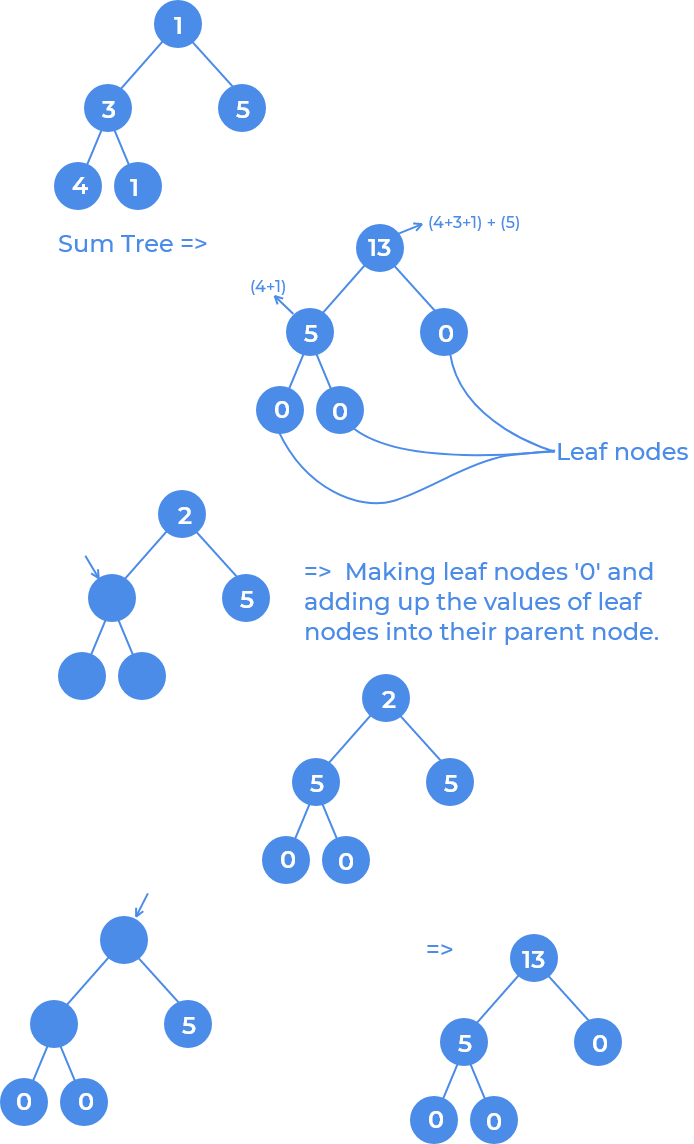
Given a binary tree and the task is to convert that tree into SumTree.
Solution Approach :
Introduction :
A SumTree is a Binary Tree where the value of a node is equal to sum of the nodes present in the left subtree and right subtree. In SumTree the leaf node values are always
0.
Approach :
We can store the sum of left & right subtree values in the root itselft, but this will result in the loss of the value which is currently stored in the root and we will be needing this value to update the parent node value.
Suppose, inorder traversal of our tree is :1 ,2 ,3, now we will store the left & right subtree values (2+3) = 5 in the root node , now the root node value is5which is wrong, the correct answer would be:2+3+1= 6
We need to store the old value (1) somewhere before replacing the this value with the new value (5), in order to return the answer i.e sum of new and old values. (5+1)
Complexity Analysis :
Since we are traversing each node atmost once, the time complexity of this approach is
O(n).
Considering the space complexity, the only space it takes is the recursion stack.
SOLUTIONS:
#include <stdio.h>
#include<stdlib.h>
#define ll long long
#define REP(i, n) for (i = 0; i < n; i++)
struct nodelist
{
ll value;
struct nodelist *left;
struct nodelist *right;
};
typedef struct nodelist node;
struct Queue
{
int front, rear, size;
unsigned capacity;
node* *array;
};
typedef struct Queue queue;
queue* createQueue(unsigned capacity)
{
queue* qu =(queue*)malloc(sizeof(queue));
qu->capacity = capacity;
qu->front = qu->size =0;
qu->rear = capacity-1;
qu->array = (node **)malloc(qu->capacity * sizeof(node));
return qu;
}
int isFull(queue* queue1)
{
return (queue1->size == queue1->capacity);
}
int isEmpty(queue* queue1)
{
return (queue1->size==0);
}
void enqueue(queue* queue1, node* item)
{
if(isFull(queue1))
return ;
queue1->rear = (queue1->rear +1 )%queue1->capacity;
queue1->array[queue1->rear] = item;
queue1->size = queue1->size +1;
}
node dequeue(queue* queue1)
{
node* item = queue1->array[queue1->front];
queue1->front = (queue1->front +1)%queue1->capacity;
queue1->size = queue1->size -1;
return *item;
}
node* front(queue* queue1)
{
return queue1->array[queue1->front];
}
node* rear(queue * queue1)
{
return queue1->array[queue1->rear];
}
node *createNode(ll value)
{
node *t= (node *) malloc(sizeof(node));
t->value = value;
t->right = t->left = NULL;
return t;
}
void deleteNode(node*t)
{
free(t);
}
void printLevelOrder(node *root)
{
if(root==NULL)
return;
queue* queue1 = createQueue(100000);
enqueue(queue1,root);
while(!isEmpty(queue1))
{
node *t = front(queue1);
printf("%lld ",t->value);
dequeue(queue1);
if(t->left != NULL)
enqueue(queue1,t->left);
if(t->right !=NULL)
enqueue(queue1, t->right);
}
}
node *replaceNegativeOne(node *root)
{
if(root==NULL ||(root->value == -1 && root->left == NULL && root->right == NULL))
return NULL;
root->left = replaceNegativeOne(root->left);
root->right = replaceNegativeOne(root->right);
return root;
}
void deleteTree(node *node1)
{
if(node1==NULL)
return;
deleteTree(node1->left);
deleteTree(node1->right);
free(node1);
}
node *createTreeByLevelTree()
{
ll n,m;
queue* queue1 = createQueue(100000);
node *root, *t;
root = NULL;
while(scanf("%lld", &n))
{
if(isEmpty(queue1))
{
root= createNode(n);
enqueue(queue1,root);
continue;
}
scanf("%lld", &m);
t = front(queue1);
dequeue(queue1);
t->left =createNode(n);
t->right=createNode(m);
if(t->left->value !=-1)
enqueue(queue1,t->left);
if(t->right->value !=-1)
enqueue(queue1,t->right);
if(isEmpty(queue1))
break;
}
return root;
}
int convertToSumTree(node *t)
{
if(t==NULL)
return 0;
int left = convertToSumTree(t->left);
int right = convertToSumTree(t->right);
int prev = t->value;
t->value = left + right;
return t->value + prev;
}
int main() {
node *root = NULL;
root = createTreeByLevelTree();
root = replaceNegativeOne(root);
convertToSumTree(root);
printLevelOrder(root);
deleteTree(root);
return 0;
}
#define REP(i, n) for (i = 0; i < n; i++)
#define pb(a) push_back(a)
#define vi vector<long>
#define ll long long
#include <bits/stdc++.h>
using namespace std;
struct node
{
ll value;
node *left;
node *right;
};
node *createNode(ll value)
{
node *t = new node();
t->value = value;
t->right = t->left = NULL;
return t;
}
void deleteNode(node *t)
{
delete t;
}
node *replaceNegativeOne(node *root)
{
if (root == NULL || (root->value == -1 && root->left == NULL && root->right == NULL))
return NULL;
root->left = replaceNegativeOne(root->left);
root->right = replaceNegativeOne(root->right);
return root;
}
void printLevelOrder(node *root)
{
if (root == NULL)
return;
queue<node *> q;
q.push(root);
while (!q.empty())
{
node *t = q.front();
cout << t->value << " ";
q.pop();
if (t->left != NULL)
q.push(t->left);
if (t->right != NULL)
q.push(t->right);
}
}
node *createTreeByLevelTree()
{
ll n, m;
queue<node *> q;
node *root, *t;
root = NULL;
while (cin >> n)
{
if (q.empty())
{
root = createNode(n);
q.push(root);
continue;
}
cin >> m;
t = q.front();
q.pop();
t->left = createNode(n);
t->right = createNode(m);
if (t->left->value != -1)
{
q.push(t->left);
}
if (t->right->value != -1)
{
q.push(t->right);
}
if (q.empty())
{
break;
}
}
return root;
}
void deleteTree(node *node)
{
if (node == NULL)
return;
deleteTree(node->left);
deleteTree(node->right);
delete node;
}
int convertToSumTree(node *root)
{
if(root==NULL)
return 0;
int left = convertToSumTree(root->left);
int right = convertToSumTree(root->right);
int prev = root->value;
root->value = left + right;
return root->value + prev;
}
int main()
{
node *root = NULL;
root = createTreeByLevelTree();
root = replaceNegativeOne(root);
convertToSumTree(root);
printLevelOrder(root);
deleteTree(root);
return 0;
}
import java.util.LinkedList;
import java.util.*;
import java.util.Scanner;
import java.io.*;
class Node
{
long value;
Node left, right;
public Node(long item)
{
value = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree() {
root = null;
}
Node createNode(long value) {
Node t = new Node(value);
return t;
}
Node replaceNegativeOne(Node root) {
if (root == null || (root.value == -1 && root.left == null && root.right == null)) {
return null;
}
root.left = replaceNegativeOne(root.left);
root.right = replaceNegativeOne(root.right);
return root;
}
public void printLevelOrder(Node root)
{
if(root==null)
{
return;
}
Queue<Node> nodes = new LinkedList<>();
nodes.add(root);
while(!nodes.isEmpty())
{
Node node = nodes.remove();
System.out.print(node.value+" ");
if(node.left!=null)
{
nodes.add(node.left);
}
if(node.right!=null)
{
nodes.add(node.right);
}
}
}
Node createTreeByLevelTree() {
Scanner sc = new Scanner(System.in);
long n, m;
Queue<Node> queue = new LinkedList<>();
Node t;
root = null;
while (sc.hasNext()) {
n = sc.nextLong();
if (queue.isEmpty()) {
root = createNode(n);
((LinkedList<Node>) queue).add(root);
continue;
}
m = sc.nextLong();
t = ((LinkedList<Node>) queue).peekFirst();
((LinkedList<Node>) queue).pop();
t.left = createNode(n);
t.right = createNode(m);
if (t.left.value != -1)
((LinkedList<Node>) queue).add(t.left);
if (t.right.value != -1)
((LinkedList<Node>) queue).add(t.right);
if (queue.isEmpty())
break;
}
return root;
}
void deleteTree(Node node) {
node = null;
}
long convertToSumTree(Node node) {
if(node==null)
return 0;
long left = convertToSumTree(node.left);
long right = convertToSumTree(node.right);
long prev = node.value;
node.value = left+right;
return node.value + prev;
}
}
public class Main {
public static void main(String[] args) {
// write your code here
BinaryTree bt = new BinaryTree();
bt.root = bt.createTreeByLevelTree();
bt.root = bt.replaceNegativeOne(bt.root);
bt.convertToSumTree(bt.root);
bt.printLevelOrder(bt.root);
bt.deleteTree(bt.root);
}
}
[forminator_quiz id="1780"]
This article tried to discuss DFS , Recursion. Hope this blog helps you understand and solve the problem. To practice more problems on DFS , Recursion you can check out .