Concepts Used
DFS , Recursion, Stack
Difficulty Level
Medium
Problem Statement :
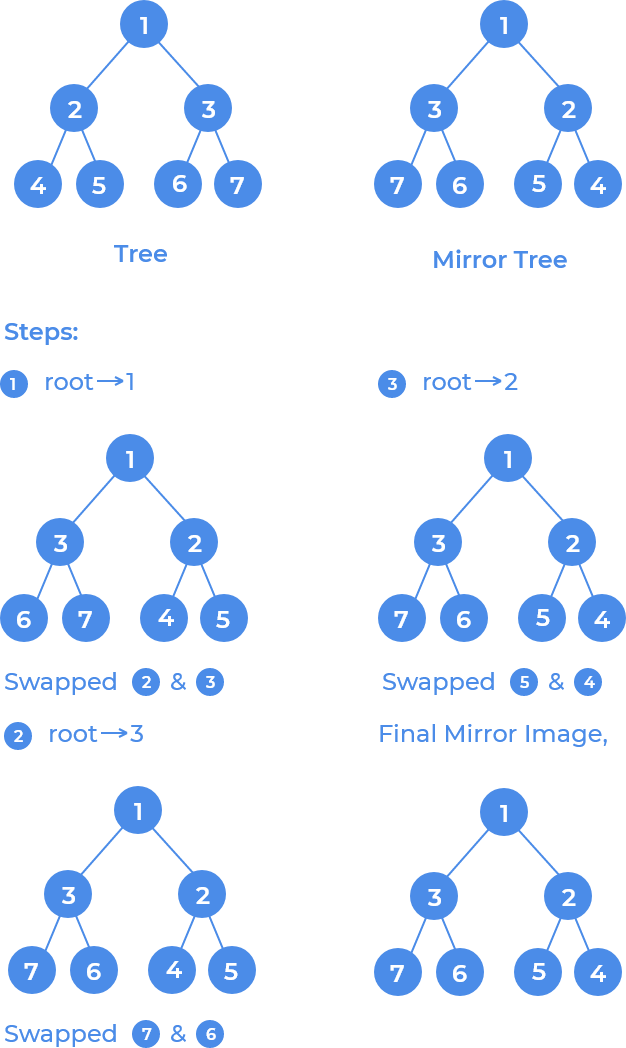
Given a Binary Tree, convert it into its mirror.
Solution Approach :
Introduction:
Idea is to swap left & right node for every root, and make every node, root, once. We can do this using recursion or stack.
Method 1 (Stack):
In this method we are using a stack
sto visit every node in Depth Firt Search fashion.
We will push our root node in the stack and perform following operation untill our stack is empty :
- Take out the topmost node and pop it after storing in a temporary node (
temp = s.top()).- swap left & right node ( swap(temp->left , temp->right) ).
- If left node (temp->left) is not null push it into the stack and do the same for right node `temp->right).
Method 2 (Recursion) :
We will use recursion to traverse our tree in Depth First Search manner to convert it into its mirror image.
Starting from the root node we will swap left and right node pointers of our tree.
We will call the same function recursively for it’s left & right subtrees untill we traverse all the nodes.
Below is the implementation in three different languagues.
Complexity Analysis :
We are visiting each node once since the time complexity would be
O(n)for the stack approach.The space complexity is
O(n)as we are using a stack of sizen, wherenis the number of nodes in tree.
Solutions:
#include <stdio.h>
#include<stdlib.h>
#define ll long long
#define REP(i, n) for (i = 0; i < n; i++)
struct nodelist
{
ll value;
struct nodelist *left;
struct nodelist *right;
};
typedef struct nodelist node;
struct Queue
{
int front, rear, size;
unsigned capacity;
node* *array;
};
typedef struct Queue queue;
queue* createQueue(unsigned capacity)
{
queue* qu =(queue*)malloc(sizeof(queue));
qu->capacity = capacity;
qu->front = qu->size =0;
qu->rear = capacity-1;
qu->array = (node **)malloc(qu->capacity * sizeof(node));
return qu;
}
int isFull(queue* queue1)
{
return (queue1->size == queue1->capacity);
}
int isEmpty(queue* queue1)
{
return (queue1->size==0);
}
void enqueue(queue* queue1, node* item)
{
if(isFull(queue1))
return ;
queue1->rear = (queue1->rear +1 )%queue1->capacity;
queue1->array[queue1->rear] = item;
queue1->size = queue1->size +1;
}
node dequeue(queue* queue1)
{
node* item = queue1->array[queue1->front];
queue1->front = (queue1->front +1)%queue1->capacity;
queue1->size = queue1->size -1;
return *item;
}
node* front(queue* queue1)
{
return queue1->array[queue1->front];
}
node* rear(queue * queue1)
{
return queue1->array[queue1->rear];
}
node *createNode(ll value)
{
node *t= (node *) malloc(sizeof(node));
t->value = value;
t->right = t->left = NULL;
return t;
}
void deleteNode(node*t)
{
free(t);
}
node *replaceNegativeOne(node *root)
{
if(root==NULL ||(root->value == -1 && root->left == NULL && root->right == NULL))
return NULL;
root->left = replaceNegativeOne(root->left);
root->right = replaceNegativeOne(root->right);
return root;
}
void deleteTree(node *node1)
{
if(node1==NULL)
return;
deleteTree(node1->left);
deleteTree(node1->right);
free(node1);
}
void inOrderTraversal(node *t)
{
//write your code here;
if (t == NULL)
return;
inOrderTraversal(t->left);
printf("%d ",t->value);
inOrderTraversal(t->right);
}
node *createTreeByLevelTree()
{
ll n,m;
queue* queue1 = createQueue(100000);
node *root, *t;
root = NULL;
while(scanf("%lld", &n))
{
if(isEmpty(queue1))
{
root= createNode(n);
enqueue(queue1,root);
continue;
}
scanf("%lld", &m);
t = front(queue1);
dequeue(queue1);
t->left =createNode(n);
t->right=createNode(m);
if(t->left->value !=-1)
enqueue(queue1,t->left);
if(t->right->value !=-1)
enqueue(queue1,t->right);
if(isEmpty(queue1))
break;
}
return root;
}
void mirror(node *root)
{
if(root== NULL)
return;
mirror(root->left);
mirror(root->right);
node * temp = root->left;
root->left = root->right;
root->right = temp;
}
int main() {
node *root = NULL;
root = createTreeByLevelTree();
root = replaceNegativeOne(root);
mirror(root);
inOrderTraversal(root);
deleteTree(root);
return 0;
}
#define REP(i, n) for (i = 0; i < n; i++)
#define pb(a) push_back(a)
#define vi vector<long>
#define ll long long
#include <bits/stdc++.h>
using namespace std;
struct node
{
ll value;
node *left;
node *right;
};
node *createNode(ll value)
{
node *t = new node();
t->value = value;
t->right = t->left = NULL;
return t;
}
void deleteNode(node *t)
{
delete t;
}
node *replaceNegativeOne(node *root)
{
if (root == NULL || (root->value == -1 && root->left == NULL && root->right == NULL))
return NULL;
root->left = replaceNegativeOne(root->left);
root->right = replaceNegativeOne(root->right);
return root;
}
node *createTreeByLevelTree()
{
ll n, m;
queue<node *> q;
node *root, *t;
root = NULL;
while (cin >> n)
{
if (q.empty())
{
root = createNode(n);
q.push(root);
continue;
}
cin >> m;
t = q.front();
q.pop();
t->left = createNode(n);
t->right = createNode(m);
if (t->left->value != -1)
{
q.push(t->left);
}
if (t->right->value != -1)
{
q.push(t->right);
}
if (q.empty())
{
break;
}
}
return root;
}
void inOrderTraversal(node *t)
{
//write your code here;
if (t == NULL)
return;
inOrderTraversal(t->left);
cout << t->value << " ";
inOrderTraversal(t->right);
}
void deleteTree(node *node)
{
if (node == NULL)
return;
deleteTree(node->left);
deleteTree(node->right);
delete node;
}
void mirror(node *a)
{
stack<node *> s;
s.push(a);
while(!s.empty())
{
node *t = s.top();
s.pop();
node* temp = t->left;
t->left = t->right;
t->right= temp;
if(t->left)
s.push(t->left);
if(t->right)
s.push(t->right);
}
}
int main()
{
node *root = NULL;
root = createTreeByLevelTree();
root = replaceNegativeOne(root);
mirror(root);
inOrderTraversal(root);
deleteTree(root);
return 0;
}
import java.util.LinkedList;
import java.util.Queue;
import java.util.*;
import java.io.*;
class Node
{
long value;
Node left, right;
public Node(long item)
{
value = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree() {
root = null;
}
Node createNode(long value) {
Node t = new Node(value);
return t;
}
Node replaceNegativeOne(Node root) {
if (root == null || (root.value == -1 && root.left == null && root.right == null)) {
return null;
}
root.left = replaceNegativeOne(root.left);
root.right = replaceNegativeOne(root.right);
return root;
}
void inOrderTraversal(Node node) {
//write your code here
if(node == null)
return;
inOrderTraversal(node.left);
System.out.print(node.value+" ");
inOrderTraversal(node.right);
}
Node createTreeByLevelTree() {
Scanner sc = new Scanner(System.in);
long n, m;
Queue<Node> queue = new LinkedList<>();
Node t;
root = null;
while (sc.hasNext()) {
n = sc.nextLong();
if (queue.isEmpty()) {
root = createNode(n);
((LinkedList<Node>) queue).add(root);
continue;
}
m = sc.nextLong();
t = ((LinkedList<Node>) queue).peekFirst();
((LinkedList<Node>) queue).pop();
t.left = createNode(n);
t.right = createNode(m);
if (t.left.value != -1)
((LinkedList<Node>) queue).add(t.left);
if (t.right.value != -1)
((LinkedList<Node>) queue).add(t.right);
if (queue.isEmpty())
break;
}
return root;
}
void deleteTree(Node node) {
node = null;
}
void mirror(Node node) {
//write your code here
if(node == null)
return ;
mirror(node.left);
mirror(node.right);
Node temp = node.left;
node.left = node.right;
node.right = temp;
}
}
public class Main {
public static void main(String[] args) {
// write your code here
BinaryTree bt = new BinaryTree();
bt.root = bt.createTreeByLevelTree();
bt.root = bt.replaceNegativeOne(bt.root);
bt.mirror(bt.root);
bt.inOrderTraversal(bt.root);
bt.deleteTree(bt.root);
}
}
[forminator_quiz id="1652"]
This article tried to discuss the concept of DFS , Recursion, Stack. Hope this blog helps you understand and solve the problem. To practice more problems on DFS , Recursion, Stack you can check out .