Introduction
The linked list is one of the most important concepts and data structures to learn while preparing for interviews. Having a good grasp of Linked Lists can be a huge plus point in a coding interview.
Problem Statement
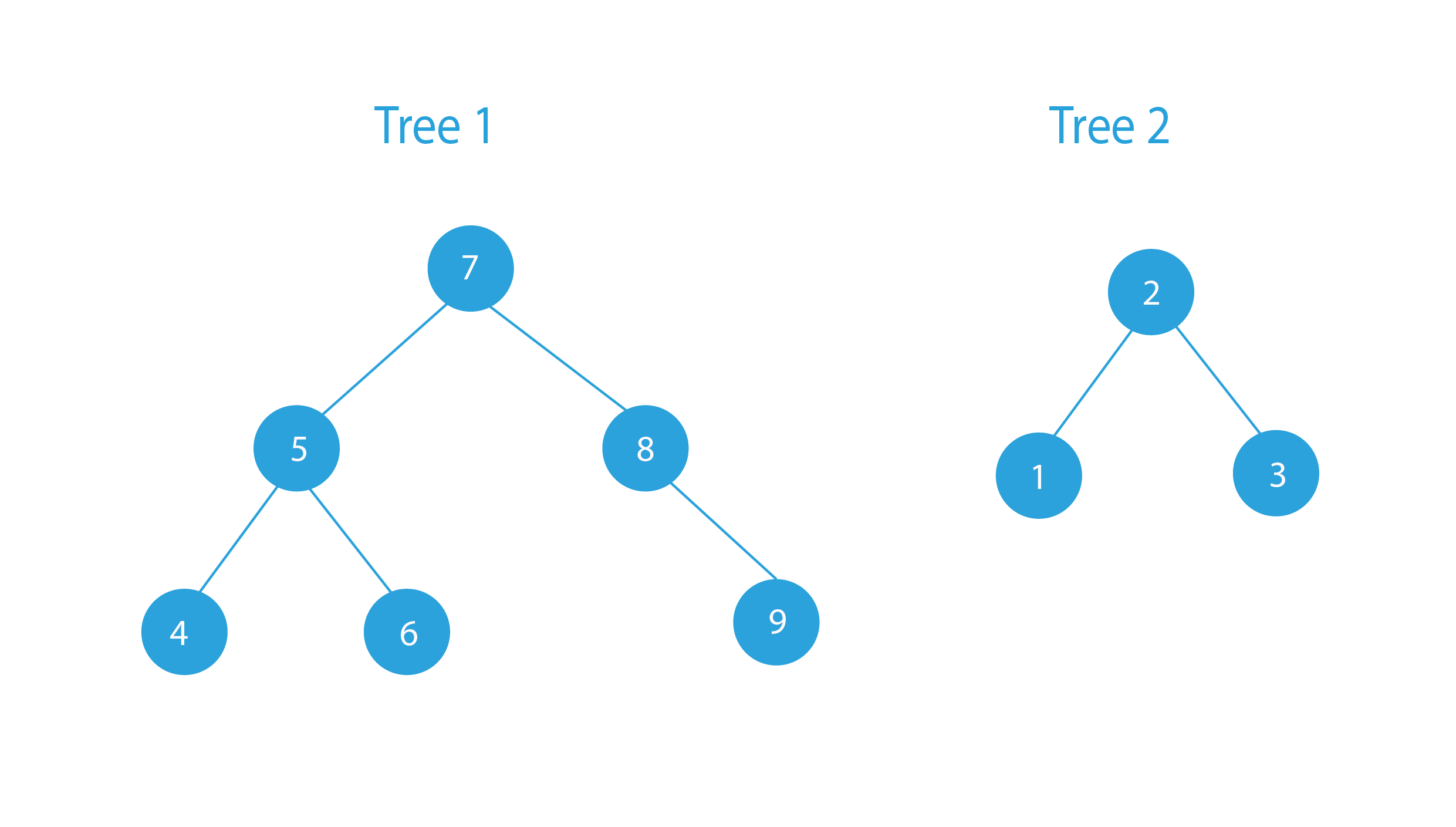
In this problem, we are given two balanced binary search trees. We have to merge these two given binary search trees to form a third balanced binary search tree.
Problem Statement Understanding
This problem requires us to create a third balanced binary search tree, which will contain all the nodes of the given two balanced binary search trees.
Sample Input:
Two Balanced Tree
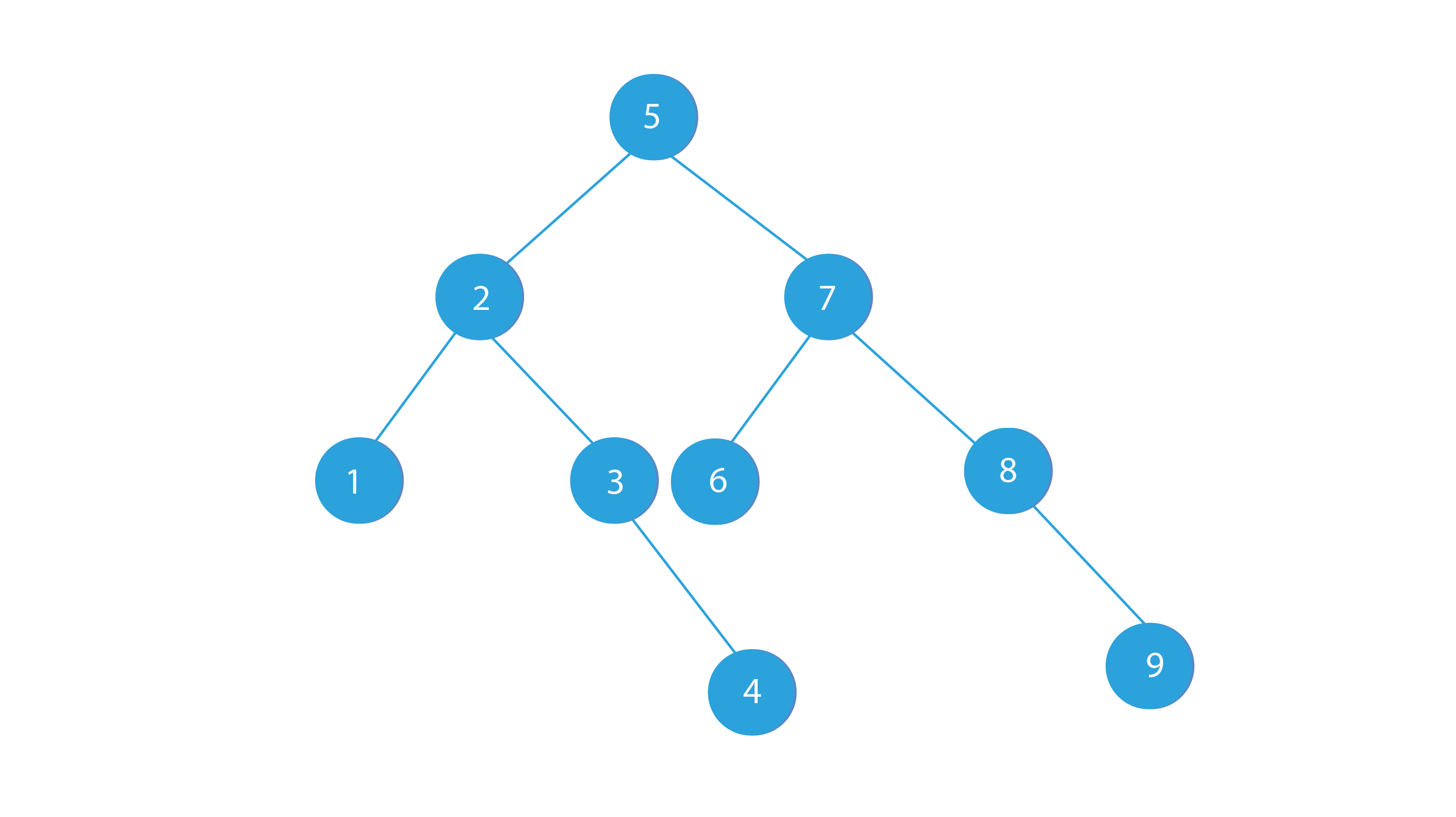
Sample Output:
Final Merged Tree
Explanation:
Both the balanced binary search trees are merged into a single binary search tree.
The first thing that comes to mind is inserting elements from tree2 to tree1, right? This is a correct approach, but the time complexity of this solution is O(Nlog(N)). Can we do better than this? Yes. Let us have a glance at the different approaches.
Approach#1
In this approach, we will take all the elements of the first binary search tree one by one, and insert them into the second binary search tree. As we know, inserting an element in a self-balancing binary search tree takes log(N) time, where N is the size of the binary search tree. To optimize the time complexity, we will pick the smaller tree as the first tree.
This method takes O(Nlog(N)) time.
Algorithm
- Traverse through the smaller BST and insert all of its elements into the second BST.
- The insertion in a BST takes O(log(N)) time, so the total time complexity of this approach is O(Nlog(N)).
Approach#2
In this approach, we are going to use a doubly-linked list to merge the given trees in place. First, we will convert the given two binary search trees into doubly-linked lists. Then, we will merge those two doubly-linked lists. Finally, we will build a balanced binary search tree from the merged doubly linked list.
This method takes O(M+N) time, M and N are the size of the trees.
Algorithm
- Convert the given two Binary Search Trees to doubly linked lists in place.
- Merge the two sorted doubly-linked lists;
- Make a balanced Binary Search Tree from the merged doubly linked list.
Approach#3
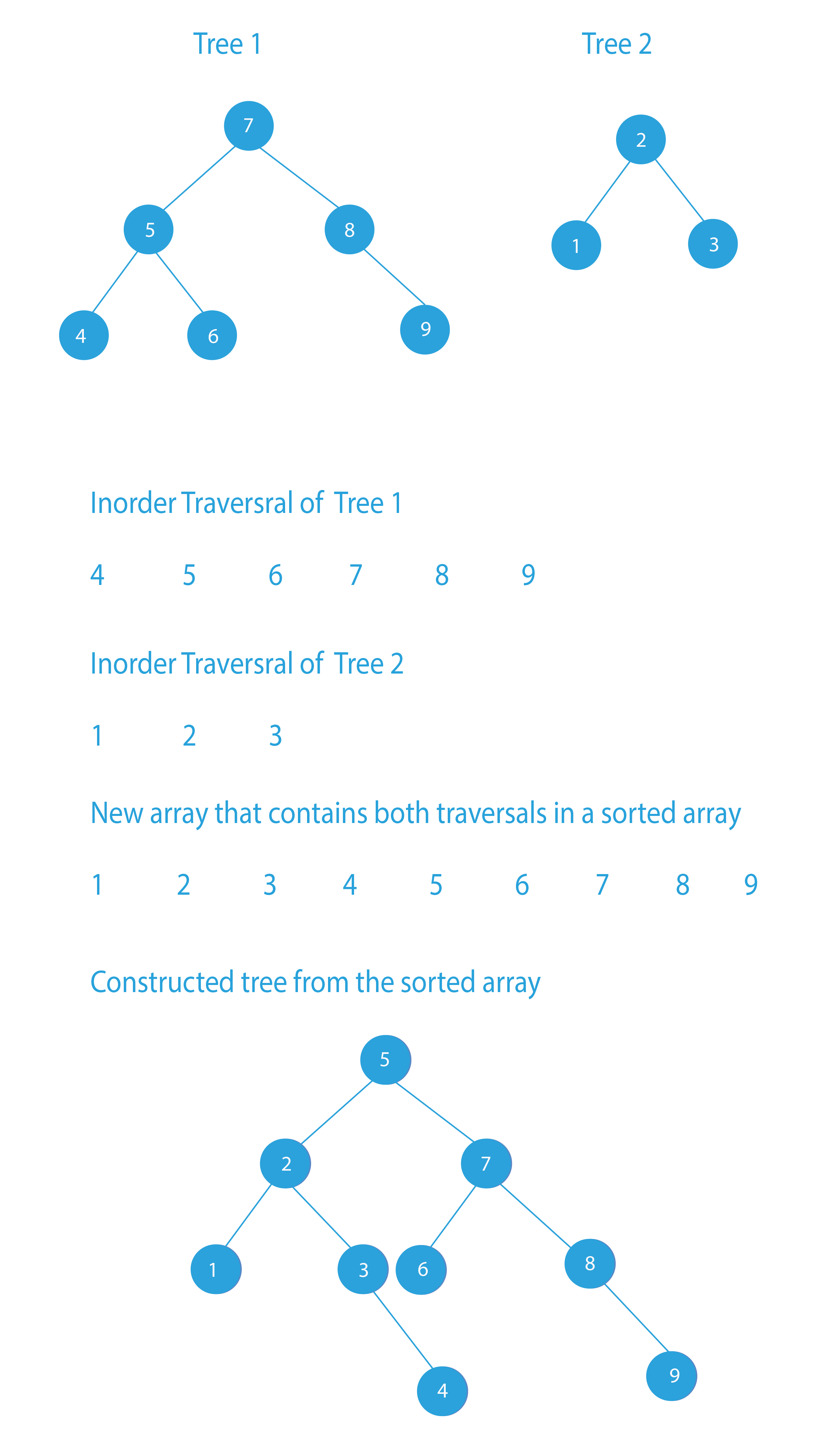
In this approach, we are going to store the in-order traversal of both the binary search trees in two arrays A_1 and A_2. Now, We will create a new array, which will contain all the elements of both A_1 and A_2 in a sorted way. Finally, we will convert the sorted array into a balanced binary search tree, hence the two binary search trees are merged.
This solution takes O(M+N) time, M and N are the size of the trees.
Algorithm
- Store the in-order traversal of both the binary search trees in two arrays, say A_1 and A_2.
- Now, create a new array A_3, and insert the elements of A_1 and A_2 in A_3, in the sorted manner.
Dry Run
Code Implementation
#includeusing namespace std; class node { public: int data; node* left; node* right; }; int *mergearray(int arr1[], int arr2[], int m, int n); void storeInorder(node* node, int inorder[], int *index_ptr); node* arrayToBST(int arr[], int start, int end); node* TreeMerge(node *root1, node *root2, int m, int n) { int *arr1 = new int[m]; int i = 0; storeInorder(root1, arr1, &i); int *arr2 = new int[n]; int j = 0; storeInorder(root2, arr2, &j); int *NewArr = mergearray(arr1, arr2, m, n); return arrayToBST (NewArr, 0, m + n - 1); } node* newNode(int data) { node* Node = new node(); Node->data = data; Node->left = NULL; Node->right = NULL; return(Node); } void printInorder(node* node) { if (node == NULL) return; printInorder(node->left); cout << node->data << " "; printInorder(node->right); } int *mergearray(int arr1[], int arr2[], int m, int n) { int *NewArr = new int[m + n]; int x = 0, y = 0, z = 0; while (x < m && y < n) { if (arr1[x] < arr2[y]) { NewArr[z] = arr1[x]; x++; } else { NewArr[z] = arr2[y]; y++; } z++; } while (x < m) { NewArr[z] = arr1[x]; x++; z++; } while (y < n) { NewArr[z] = arr2[y]; y++; z++; } return NewArr; } void storeInorder(node* node, int inorder[], int *index_ptr) { if (node == NULL) return; storeInorder(node->left, inorder, index_ptr); inorder[*index_ptr] = node->data; (*index_ptr)++; storeInorder(node->right, inorder, index_ptr); } node* arrayToBST(int arr[], int start, int end) { if (start > end) return NULL; int mid = (start + end)/2; node *root = newNode(arr[mid]); root->left = arrayToBST(arr, start, mid-1); root->right = arrayToBST(arr, mid+1, end); return root; } int main() { node *root1 = newNode(7); root1->left = newNode(5); root1->right = newNode(8); root1->left->left = newNode(4); root1->left->right = newNode(6); root1->right->right = newNode(9); node *root2 = newNode(2); root2->left = newNode(1); root2->right = newNode(3); node *mergedTree = TreeMerge(root1, root2, 6, 3); cout << "Following is Inorder traversal of the merged tree \n"; printInorder(mergedTree); return 0; }
import java.io.*;
import java.util.ArrayList;
class Node {
int data;
Node left, right;
Node(int d) {
data = d;
left = right = null;
}
}
public class BinarySearchTree
{
Node root;
BinarySearchTree() {
root = null;
}
void inorder()
{
inorderUtil(this.root);
}
void inorderUtil(Node node)
{
if(node==null)
return;
inorderUtil(node.left);
System.out.print(node.data + " ");
inorderUtil(node.right);
}
public ArrayList storeInorderUtil(Node node, ArrayList list)
{
if(node == null)
return list;
storeInorderUtil(node.left, list);
list.add(node.data);
storeInorderUtil(node.right, list);
return list;
}
ArrayList storeInorder(Node node)
{
ArrayList list1 = new ArrayList<>();
ArrayList list2 = storeInorderUtil(node,list1);
return list2;
}
ArrayList merge(ArrayListlist1, ArrayListlist2, int m, int n)
{
ArrayList list3 = new ArrayList<>();
int i=0;
int j=0;
while( ilist, int start, int end)
{
if(start > end)
return null;
int mid = (start+end)/2;
Node node = new Node(list.get(mid));
node.left = ALtoBST(list, start, mid-1);
node.right = ALtoBST(list, mid+1, end);
return node;
}
Node mergeTrees(Node node1, Node node2)
{
ArrayListlist1 = storeInorder(node1);
ArrayListlist2 = storeInorder(node2);
ArrayListlist3 = merge(list1, list2, list1.size(), list2.size());
Node node = ALtoBST(list3, 0, list3.size()-1);
return node;
}
public static void main (String[] args)
{
BinarySearchTree tree1 = new BinarySearchTree();
tree1.root = new Node(7);
tree1.root.left = new Node(5);
tree1.root.right = new Node(8);
tree1.root.left.left = new Node(4);
tree1.root.left.right = new Node(6);
tree1.root.right.right = new Node(9);
BinarySearchTree tree2 = new BinarySearchTree();
tree2.root = new Node(2);
tree2.root.left = new Node(1);
tree2.root.right = new Node(3);
BinarySearchTree tree = new BinarySearchTree();
tree.root = tree.mergeTrees(tree1.root, tree2.root);
System.out.println("The Inorder traversal of the merged BST is: ");
tree.inorder();
}
}
Output:
Following is Inorder traversal of the merged tree
1 2 3 4 5 6 7 8 9
Time Complexity: O(M+N), traversal of both the trees is required.
Space Complexity: O(M+N), the space needed to create the new array and tree.
So, in this article, we have tried to explain the most efficient approach to merge two balanced binary trees. The solution to this problem requires a good grasp of some other basic concepts. Thus, this is an important problem for coding interviews. If you want to solve more questions on Linked List, which are curated by our expert mentors at PrepBytes, you can follow this link Linked List.