Concepts Used
Strings, Hash Table
Difficulty Level
Hard
Problem Statement (Simplified):
Find the total number of children standing on each square after 10100 rotations by every individual child. Each child moves according to
'R'or'L'written on each square. WhereRstands for right andLstands for left.
Test Case
Input:
RRLRL
Output:
0 1 2 1 1
Explanation:
After each child had moved one place to their left or right as written on their square, their final count becomes
0 2 1 1 1
Now 2 children are standing on 2nd square and 1 square on 3rd, 4th and 5th square each. After repeating the same procedure for 10^100 steps, their final position becomes,
0 1 2 1 1Solving Approach :
Bruteforce Approach :
1) We can move each child by direction written on his square, after all, children have moved, we repeat this step for 10100 times. After all, steps have completed, we print final counts.
2) By looking above approach we can see it would take infinite time even to process an array of smaller length. As compiler takes 1 second to process10^{7}procedures, so this program takes O(N\times{10100 }) time to solve this problem for an array of sizeN.
3) We can’t solve this problem with this approach, so we look for a more efficient approach.
Efficient Approach :
1) We know whenever the square direction is changed from
LefttoRightorRighttoLeft, i.e. when adjacent squares have a different direction, the child will rotate circularly for all next steps in these both squares. It will repeat its position after every 2 rotations in these two squares.
2) So if we can identify when the nextLeftwill be for the current square which directs toRightor when was the previousRightfor the current square which directsLeft, We can solve this problem easily.
3) For a child standing on the square which directs toRight
- Child will be standing on the first square stating
Leftfrom its position if the distance between its initial position and nextLeftsquare iseven.- The position will be one less if the distance between its initial position and next
Leftsquare isodd.
4) For a child standing on the square which directs toLeft- Child will be standing on last square stating
Rightbefore it’s the position if the distance between its initial position and previousRightsquare iseven.- The position will be one closer if the distance between its initial position and previous
Rightsquare isodd.
Example
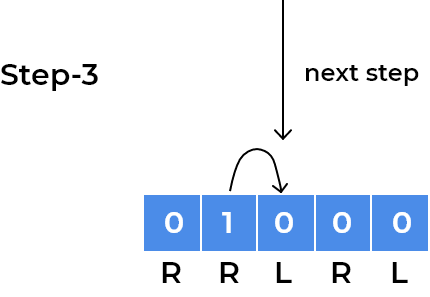
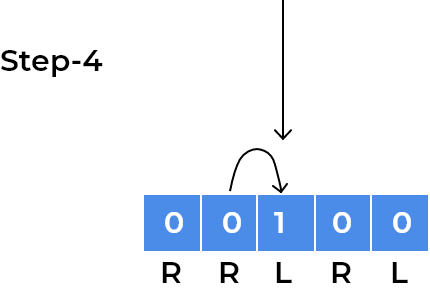
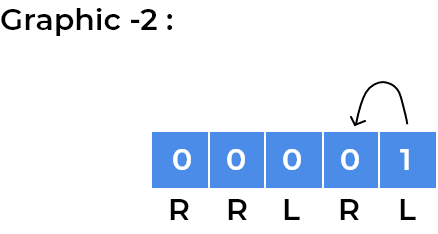
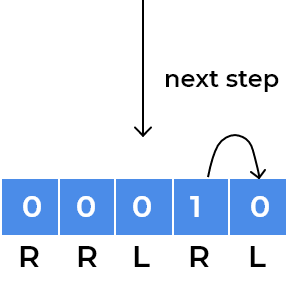
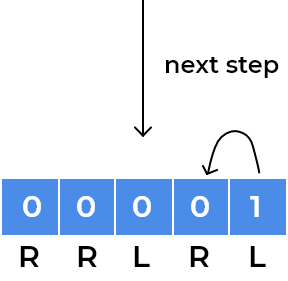
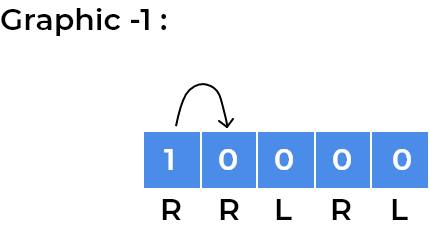
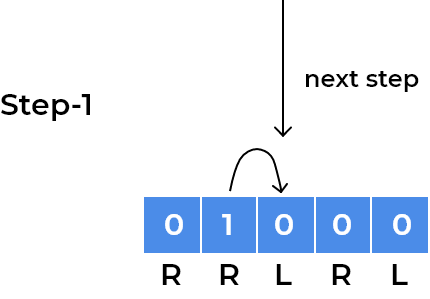
- We can visualise above approach using an example. So let’s take the initial example we discussed in the test case section.
- Our squares have
RRLRLwritten. As every child moves according to direction written on the square, we can focus on a single child for understanding patterns.- Let’s see movements for the child standing at index 0.
- We can see the child has now gone into a loop where it is stuck at index
1and2depending on the step number. After every 2 steps, it repeats its position. We observe the same for the child standing onleftsquare initially, for example, we can visualise same for the child standing at last square.
- We can observe children will rotate in the loop whenever the direction of adjacent squares will change.
- We can maintain an array which saves next
Leftindex and one for saving previousRightindex occurring for the current element.- As mentioned in the efficient approach we can further calculate the position of the current child. For example, a child standing at index
0will have nextLeftat index2. So we will calculate the distance between both of them and check if it isevenoroddand we’ll get final position for the child.- We’ll increase the count in the hash table by 1, where the final position will be the index of the hash table.
- So final answer become
0 1 2 1 1.
Solutions
#include<stdio.h>
#include<string.h>
#define maxn 100010
char s[maxn];
int n, ans[maxn], nxtL[maxn], preR[maxn];
int main()
{
scanf("%s", s);
n = strlen(s);
int i;
for (i = 1; i < n; ++i)
if (s[i] == 'R')
preR[i] = i;
else preR[i] = preR[i - 1];
for (i = n - 1; i >= 0; --i)
if (s[i] == 'L')
nxtL[i] = i;
else nxtL[i] = nxtL[i + 1];
int step;
for (i = 0; i < n; ++i) {
if (s[i] == 'R') {
step = (nxtL[i] - i) & 1;
++ans[nxtL[i] - step];
} else {
step = (i - preR[i]) & 1;
++ans[preR[i] + step];
}
}
for (i = 0; i < n; ++i)
printf("%d ", ans[i]);
return 0;
}
#include<bits/stdc++.h>
#define maxn 100010
using namespace std;
char s[maxn];
int n, ans[maxn], nxtL[maxn], preR[maxn];
int main()
{
cin>>s;
n = strlen(s);
int i;
for (i = 1; i < n; ++i)
if (s[i] == 'R')
preR[i] = i;
else preR[i] = preR[i - 1];
for (i = n - 1; i >= 0; --i)
if (s[i] == 'L')
nxtL[i] = i;
else nxtL[i] = nxtL[i + 1];
int step;
for (i = 0; i < n; ++i) {
if (s[i] == 'R') {
step = (nxtL[i] - i) & 1;
++ans[nxtL[i] - step];
} else {
step = (i - preR[i]) & 1;
++ans[preR[i] + step];
}
}
for (i = 0; i < n; ++i)
cout<<ans[i]<<" ";
return 0;
}
import java.util.*;
import java.io.*;
public class Main {
public static void main(String args[]) throws IOException {
Scanner sc= new Scanner(System.in);
String s = sc.next();
int n = s.length();
int ans[] = new int[100010];
int nxtL[] = new int[100010];
int preR[] = new int[100010];
int i;
for (i = 1; i < n; ++i)
if (s.charAt(i) == 'R')
preR[i] = i;
else preR[i] = preR[i - 1];
for (i = n - 1; i >= 0; --i)
if (s.charAt(i) == 'L')
nxtL[i] = i;
else nxtL[i] = nxtL[i + 1];
int step;
for (i = 0; i < n; ++i) {
if (s.charAt(i) == 'R') {
step = (nxtL[i] - i) & 1;
++ans[nxtL[i] - step];
} else {
step = (i - preR[i]) & 1;
++ans[preR[i] + step];
}
}
for (i = 0; i < n; ++i)
System.out.print(ans[i]+" ");
}
}
maxn = 100010
s = [""] * maxn
ans = [0] * maxn
nxtL = [0] * maxn
preR = [0] * maxn
s = input()
n = len(s)
for i in range(1, n):
if (s[i] == 'R'):
preR[i] = i
else:
preR[i] = preR[i - 1]
for i in range(n - 1, -1, -1):
if (s[i] == 'L'):
nxtL[i] = i
else:
nxtL[i] = nxtL[i + 1]
for i in range(n):
if (s[i] == 'R'):
step = (nxtL[i] - i) & 1
ans[nxtL[i] - step] += 1
else:
step = (i - preR[i]) & 1;
ans[preR[i] + step] += 1
print(*ans[:n])
[forminator_quiz id="795"]
Space Complexity of this approach would be O(N).
This article tried to discuss Strings, Hash Table. Hope this blog helps you understand and solve the problem. To practice more problems on Strings, Hash Table you can check out .




2020/06/Graphic-1-3.png)