Sort in a unique way

Last Updated on March 30, 2022 by Ria Pathak

Concepts Used:

Sorting

Difficulty Level:

Easy

Problem Statement (Simplified):

For a given array find the length of largest sorted sub-array in it, but if the current array is not sorted, we divide the array into two halves and then check them for sorting.

See original problem statement here

Test Case:

Input:
1
8
11 12 1 2 13 14 3 4

Output:
2

Explanation:
Sorted sub arrays are [11,12], [1,2], [13,14] and [3,4]. Maximum size is 2. So our answer is 2.

Solving Approach :

Bruteforce Approach:

1) We can divide array recursively, and check if the current subarray is sorted or not,. If yes, we return the length of the sub-array. Parent array returns the maximum of the values returned from its sub-arrays or its length if the parent array is sorted.

2) Dividing array takes O(log(N)) time, for each array we get, we check if it is sorted or not, where it takes another O(N) time. So, whole approach take O(N² x Log(N) ) time. This approach takes a longer time to process an array with a larger number of elements, so we move to a better and efficient approach.

Efficient Approach:

1) We can use recursion to solve this problem, by dividing the current array into two halves recursively and return 1 when the array size is 1 as an array of size 1 is already sorted.

2) Every subarray returns the length of the largest sorted sub-array of it.

3) If we receive the same lengths from both sub-arrays, we check if the last element of the left sub-array is less than the starting element of the right sub-array.

4) From the above conditions, we can observe that both sub-arrays are sorted and also the whole parent array is sorted, so we return the length of the parent array.

5) If not, we compare length received from both sub-arrays and return the maximum of both lengths received.

EXAMPLE:

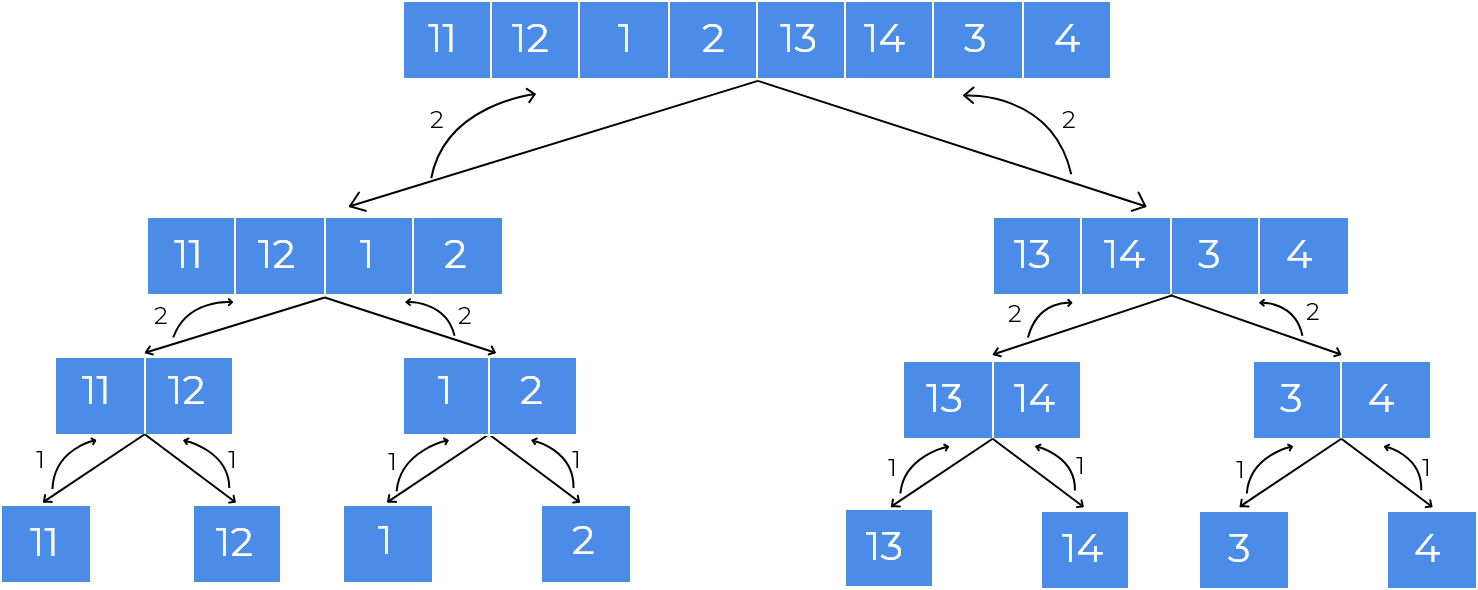
• Let array A be [11, 12 ,1 ,2 ,13 ,14 , 3, 4],

• Recursion tree according to Efficient Approach for the above array would be,

• When the array is reduced to size 1, it returns 1, as it is already sorted, as we can see in all leaf nodes in above figure.

• When two nodes return values, parent node returns the maximum of values returned from its child nodes, if both values are the same as the length of child nodes, we check if the last element of the left child is smaller than the first element of the right child. If yes, we return the sum of both child nodes.

Solutions:

#include<stdio.h>

int sortCheck(int arr[], int start, int end){
  if(start+1==end)
    return 1;
  int mid = (start+end)/2;
  int h1 = sortCheck(arr,start,mid);
  int h2 = sortCheck(arr,mid,end);
  if(h1==h2 && h1==(end-start)/2 && arr[mid-1]<=arr[mid])
    return end-start;
  if(h1>h2)
    return h1;
  else
    return h2;
}

int main(){
  int test;
  scanf("%d",&test);

  while(test--){
    int n;
    scanf("%d",&n);

    int arr[n];

    for(int i=0; i<n;i++)
      scanf("%d",&arr[i]);

    printf("%d\n",sortCheck(arr,0,n));
  }
}

#include<bits/stdc++.h>
using namespace std;

int sortCheck(int arr[], int start, int end){
  if(start+1==end)
    return 1;
  int mid = (start+end)/2;
  int h1 = sortCheck(arr,start,mid);
  int h2 = sortCheck(arr,mid,end);
  if(h1==h2 && h1==(end-start)/2 && arr[mid-1]<=arr[mid])
    return end-start;
  return max(h1,h2);
}

int main(){
  int test;
  cin>>test;

  while(test--){
    int n;
    cin>>n;

    int arr[n];

    for(int i=0; i<n;i++)
      cin>>arr[i];

    cout<<sortCheck(arr,0,n)<<endl;
  }
}

import java.util.*;
import java.io.*;

public class Main {

  static int sortCheck(int arr[], int start, int end){
    if(start+1==end)
      return 1;
    int mid = (start+end)/2;
    int h1 = sortCheck(arr,start,mid);
    int h2 = sortCheck(arr,mid,end);
    if(h1==h2 && h1==(end-start)/2 && arr[mid-1]<=arr[mid])
      return end-start;
    if(h1>h2)
      return h1;
    else
      return h2;
  }


  public static void main(String args[]) throws IOException {

    Scanner sc = new Scanner(System.in);
    int test = sc.nextInt();

    while(test--!=0){
      int n = sc.nextInt();

      int arr[] = new int[n];

      for(int i=0; i<n;i++)
        arr[i] = sc.nextInt();

      System.out.println(sortCheck(arr,0,n));
    }

  }
}

def sortCheck(arr, start, end):
	
	if(start + 1 == end):
		return 1
	
	mid = (start + end) // 2
	h1 = sortCheck(arr, start, mid)
	h2 = sortCheck(arr, mid, end)
	
	if(h1 == h2 and h1 == (end - start) // 2 and arr[mid - 1] <= arr[mid]):
		return end-start
	
	return max(h1, h2)
	

for _ in range(int(input())):

	n = int(input())
	a = list(map(int, input().split()))
	
	print(sortCheck(a, 0, n))

[forminator_quiz id="1041"]

This article tried to discuss the concept of sorting. Hope this blog helps you understand and solve the problem. To practice more problems on sorting you can check out MYCODE | Competitive Programming.