Concepts Used:
Sorting
Difficulty Level:
Easy
Problem Statement (Simplified):
Find how many elements change their place after sorting array.
Test case:
Input:
1
5
8 4 2 1 9
Output:
4
Explanation:
On sorting array, the array becomes [1 2 4 8 9] and we can see 1,2,4 and 8 have a different places in the given array. So 4 is our answer.Solving Approach :
Observation: We can see that size of array can go from 1 to 106, in worse conditions let the size of the array be 106 if we sort this array using any of sorting techniques i.e. Bubble Sort, Insertion Sort, Selection sort. They all take O(N2) in worst cases, which results in 1012 iterations when the size of the array is 106. So we, can’t choose the above three sorting algorithms. We use Merge Sort to sort array as it sorts array in linearithmic time complexity (N x log(N)) where N is size of array.
- We make a duplicate array, which will be sorted. After sorting we count number of elements which differe at same index.
Example:
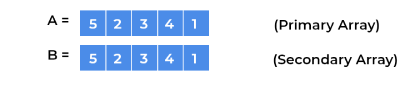
Let array
Abe,
We need to find how many elements stays at their place after sorting, So we maintain a
Secondary Arraywhich is copy of our primary arra.
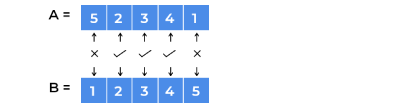
After Sorting
Secondary Array,Secondary Arraybecomes
Now, we compare both arrays, element by element and count array elements which are different at same index in both arrays.
Here, we can see
5and1are not at their same place, so our answer is2.
Solutions:
#include <stdio.h>
void merge(int arr[], int start, int mid, int end){
int left[mid-start+1];
int right[end-mid];
for(int i=start; i<mid+1; i++){
left[i-start] = arr[i];
}
for(int i=mid+1; i<=end; i++){
right[i-(mid+1)] = arr[i];
}
int leftIndex=0, rightIndex=0, arrIndex=start;
for( ; leftIndex<=mid-start && rightIndex<end-mid; arrIndex++){
if(left[leftIndex]<right[rightIndex]){
arr[arrIndex] = left[leftIndex++];
}
else{
arr[arrIndex] = right[rightIndex++];
}
}
while(leftIndex<=mid-start){
arr[arrIndex++] = left[leftIndex++];
}
while(rightIndex<end-mid){
arr[arrIndex++] = right[rightIndex++];
}
}
void mergeSort(int arr[], int start, int end){
if(end==start)
return;
mergeSort(arr,start,(start+end)/2);
mergeSort(arr,((start+end)/2)+1,end);
merge(arr,start,(start+end)/2,end);
}
int main()
{
int test;
scanf("%d",&test);
while(test--){
int n;
scanf("%d",&n);
int arr[n];
int sorted[n];
for(int i=0; i<n; i++){
scanf("%d",&arr[i]);
sorted[i] = arr[i];
}
//Sorting array
mergeSort(sorted,0,n-1);
int count = 0;
for(int i=0; i<n; i++)
if(arr[i]!=sorted[i])
count++;
printf("%d\n",count);
}
}
#include <bits/stdc++.h>
using namespace std;
void merge(int arr[], int start, int mid, int end){
int left[mid-start+1]={0};
int right[end-mid]={0};
for(int i=start; i<mid+1; i++){
left[i-start] = arr[i];
}
for(int i=mid+1; i<=end; i++){
right[i-(mid+1)] = arr[i];
}
int leftIndex=0, rightIndex=0, arrIndex=start;
for( ; leftIndex<=mid-start && rightIndex<end-mid; arrIndex++){
if(left[leftIndex]<right[rightIndex]){
arr[arrIndex] = left[leftIndex++];
}
else{
arr[arrIndex] = right[rightIndex++];
}
}
while(leftIndex<=mid-start){
arr[arrIndex++] = left[leftIndex++];
}
while(rightIndex<end-mid){
arr[arrIndex++] = right[rightIndex++];
}
}
void mergeSort(int arr[], int start, int end){
if(end==start)
return;
mergeSort(arr,start,(start+end)/2);
mergeSort(arr,((start+end)/2)+1,end);
merge(arr,start,(start+end)/2,end);
}
int main()
{
int test;
cin>>test;
while(test--){
int n;
cin>>n;
int arr[n];
int sorted[n];
for(int i=0; i<n; i++){
cin>>arr[i];
sorted[i] = arr[i];
}
//Sorting array
mergeSort(sorted,0,n-1);
int count = 0;
for(int i=0; i<n; i++)
if(arr[i]!=sorted[i])
count++;
cout<<count<<endl;
}
}
import java.util.*;
import java.io.*;
public class Main {
static void merge(int arr[], int start, int mid, int end){
int left[] = new int[mid-start+1];
int right[] = new int[end-mid];
for(int i=start; i<mid+1; i++){
left[i-start] = arr[i];
}
for(int i=mid+1; i<=end; i++){
right[i-(mid+1)] = arr[i];
}
int leftIndex=0, rightIndex=0, arrIndex=start;
for( ; leftIndex<=mid-start && rightIndex<end-mid; arrIndex++){
if(left[leftIndex]<right[rightIndex]){
arr[arrIndex] = left[leftIndex++];
}
else{
arr[arrIndex] = right[rightIndex++];
}
}
while(leftIndex<=mid-start){
arr[arrIndex++] = left[leftIndex++];
}
while(rightIndex<end-mid){
arr[arrIndex++] = right[rightIndex++];
}
}
static void mergeSort(int arr[], int start, int end){
if(end==start)
return;
mergeSort(arr,start,(start+end)/2);
mergeSort(arr,((start+end)/2)+1,end);
merge(arr,start,(start+end)/2,end);
}
public static void main(String args[]) throws IOException {
Scanner sc = new Scanner(System.in);
int test = sc.nextInt();
while(test--!=0){
int n = sc.nextInt();
int arr[] = new int[n];
int sorted[] = new int[n];
for(int i=0; i<n; i++){
arr[i] = sc.nextInt();
sorted[i] = arr[i];
}
//Sorting array
mergeSort(sorted,0,n-1);
int count = 0;
for(int i=0; i<n; i++)
if(arr[i]!=sorted[i])
count++;
System.out.println(count);
}
}
}
def merge(arr, start, mid, end): left = [0 for i in range(mid - start + 1)] right = [0 for i in range(end - mid)] for i in range(start, mid + 1): left[i - start] = arr[i] for i in range(mid + 1, end + 1): right[i - (mid + 1)] = arr[i] leftIndex = 0 rightIndex = 0 arrIndex = start while leftIndex <= mid - start and rightIndex < end - mid: if(left[leftIndex] < right[rightIndex]): arr[arrIndex] = left[leftIndex] leftIndex += 1 else: arr[arrIndex] = right[rightIndex] rightIndex += 1 arrIndex += 1 while(leftIndex <= mid - start): arr[arrIndex] = left[leftIndex] leftIndex += 1 arrIndex += 1 while(rightIndex < end - mid): arr[arrIndex] = right[rightIndex] rightIndex += 1 arrIndex += 1 def mergeSort(arr, start, end): if(end == start): return mergeSort(arr, start, (start + end) // 2) mergeSort(arr, ((start + end) // 2) + 1, end) merge(arr, start, (start + end) // 2, end) for _ in range(int(input())): n = int(input()) arr = list(map(int, input().split())) sorted = arr.copy() mergeSort(sorted, 0, n - 1) count = 0 for i in range(n): if arr[i] != sorted[i]: count += 1 print(count)
[forminator_quiz id="1075"]
So, in this blog, we have tried to explain how many elements change their place after sorting array. If you want to solve more questions on Sorting, which are curated by our expert mentors at PrepBytes, you can follow this link Sorting.