Recursive selection sort for singly linked list | Swapping node links

Last Updated on November 14, 2022 by Prepbytes

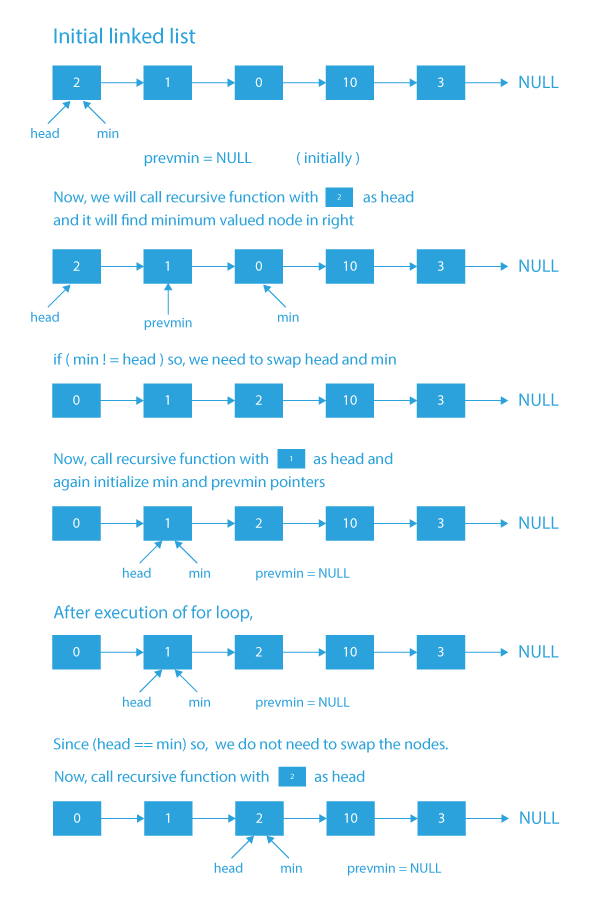
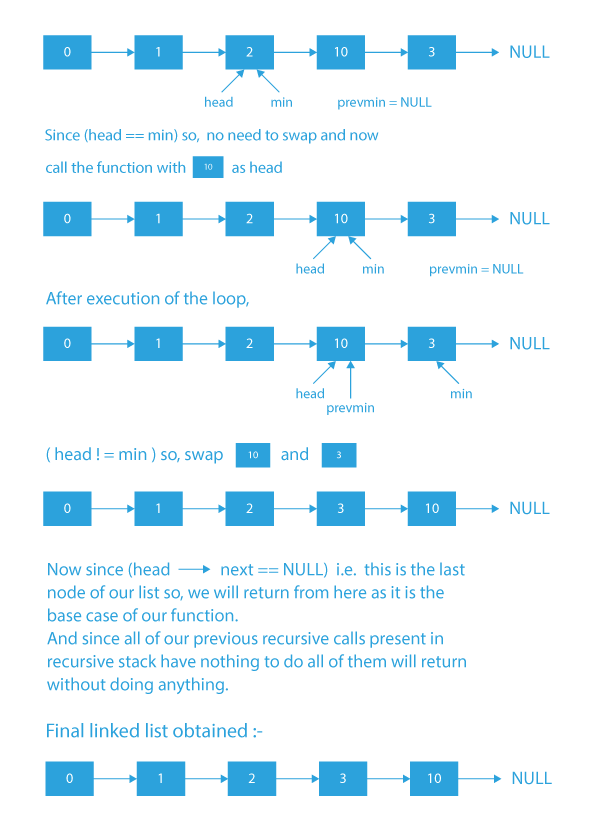
This blog consists of what is selection sort, dry run for performing selection sort, algorithm and implementation of recursive selection sort in linked list. Let’s discuss recursive selection sort in linked list in detail.

How To Perform Recursive Selection Sort In Linked List

In this problem, we will be given an unsorted linked list, and we need to sort it with the help of the selection sort algorithm recursively by referring to the best website to learn c language.

The problem statement is relatively straightforward, we will get a linked list as input, and we will have to sort it in ascending order using recursive selection sort.

Let’s try to understand it more clearly using an example.

• Let the input list given to us be:

• Now, we need to perform sorting on the above list and rearrange the list’s nodes accordingly to get a sorted list as output.
• So, after sorting, the newly formed list will be :

Note: There are various sorting algorithms to do this task, but here in the problem statement, it is explicitly mentioned that we need to perform recursive selection sort. So, we will be performing that to get desired output.

Now the main question is what is Selection sort and how does it work?

Let’s find our answers in the next section.

Selection Sort

Let us first understand how selection sort works on an array:

• We start from the first element of the array and find the minimum element in the array to the right of this element (including the current element).
• Once we found the minimum element, we swap that minimum element with our current position element.
• Then repeat the above steps for all elements of array except last element because it would be automatically placed at its correct position after execution of above steps for elements till second last position.

Let’s formulate the above steps in an algorithm:

• We will write a for loop that will iterate from the first to second last element of the array. Inside the for loop, we will perform the below three steps (step 1 to 3) for every array element.
  1) Create a min variable and initialize it with the current element.
  2) Then iterate on the array starting from the next position of the current element and update the min variable if an element less than min is found.
  3) After the loop ends, swap current element with the minimum element min.

After all the above steps have been executed, we will have our array sorted.

Note: Remember inside the for loop when you are at certain position i, the subarray left to i, starting from first position to the (i-1)^th position will be sorted while the subarray right to i starting from i to the last index of the array will be unsorted.

Dry Run For Performing Recursive Selection Sort In Linked List

Now I think from the above explanation, you got a pretty good idea of how the selection sort works.

Let’s see under the approach section how we will use Recursive Selection Sort to sort a singly linked list.

Approach For Performing Recursive Selection Sort In Linked List

Our approach will be simple:

• We need to perform recursive sorting (N-1) times, where N is the number of nodes present in the list. The reason we are performing it (N-1) times is that because after recursively sorting the list (N-1) times, (N-1) nodes of the list will be at their correct position as per the sorted linked list (As N-1 nodes are at their correct position so will be the N^th node and hence the final list will be sorted).
• Each time, we need to find the minimum node on the right of the current node and then swap the current node with it.
• Also remember to store the address of the node just before the minimum valued node because it will help while interchanging links between nodes while swapping.

Now, let’s formulate an algorithm based on the approach discussed above and handle the edge cases that might be present while implementing the code.

Algorithm For Performing Recursive Selection Sort In Linked List

• Base case: When the current node is the last node of the list, return the node.
• Initialize a pointer min with the current node and pointer beforemin with NULL. Pointer min will store the address of the node with the minimum value on the right side of the current node, and beforemin will store the address of the previous node of min.
• Once we get the min node, check if it is not the same with the node with which it was initialized. If not, then swap the current node with the min valued node.
• Call the same recursive function for the next node and return the current node once the recursive call is completed.

Code Implementation For Performing Recursive Selection Sort In Linked List

#include
using namespace std;
class Node
{
    public:
    int data;
    Node* next;
    Node(int x){
        data = x;
   next = NULL;
    }
};
void printList(Node *head)
{
    if (!head)
        return;
     
    while (head->next != NULL)
    {
        cout << head->data << " -> ";
        head = head->next;
    }
    cout << head->data << endl;
}
 
void swapNodes(struct Node** head_ref, struct Node* currX,
               struct Node* currY, struct Node* prevY)
{
    // now the head will be currY
    *head_ref = currY;
 
    // modify the link between prevY and currX
    prevY->next = currX;
 
    // swap both the nodes i.e., currX and currY
    struct Node* temp = currY->next;
    currY->next = currX->next;
    currX->next = temp;
}
 
 
 Node* selectionSort( Node* head)
{
    // when last node is reached return it
    if (head->next == NULL)
        return head;
 
    // initialize min pointer with current node which will store
    // address of minimum valued node
     Node* min = head;
 
    // initialize beforeMin pointer with current node which will
    // store address of previous node pointed by min 
     Node* beforeMin = NULL;
     Node* ptr;
 
    // search in right part of list for minimum value
    for (ptr = head; ptr->next != NULL; ptr = ptr->next) {
 
        // if true, then update 'min' and 'beforeMin'
        if (ptr->next->data < min->data) {
            min = ptr->next;
            beforeMin = ptr;
        }
    }
 
    // if min is not same as the current node then
    // swap the head node with the 'min' node
    if (min != head)
        swapNodes(&head, head, min, beforeMin);
 
    // call the recursive function for rest of the list
    head->next = recurSelectionSort(head->next);
 
    return head;
}
 
int main(void)
{
    Node* head = NULL;
    head = new Node(2);
    head->next = new Node(1);
    head->next->next = new Node(0);
    head->next->next->next = new Node(10);
    head->next->next->next->next = new Node(3);
    
    Node *tmp = selectionSort(head);
    printList(tmp);
    return 0;
}

Output

0,1,2,3,10

Time Complexity For Performing Recursive Selection Sort In Linked List: O(n²), where n is the number of nodes in the list.

Hence, we have discussed in detail for performing a recursive selection sort in linked list. Practicing linked list will boost problem solving and logical skills and having knowledge about data structures like linked list also help in the technical interviews, you can follow this link Linked List.

FAQs

1. What is the recursive selection sort?

Selection Sort is one of the sorting algorithms used to sort data by iterating an array from the beginning and replacing each element with the smallest element in the list. As we move forward the left array is sorted, and the right array is unsorted.


2. What is a recursive method?

A method or algorithm that invokes itself one or more times with different arguments.


3. Why is recursion difficult?

The key reason is that we are looking at the same function with different values of local variables. It is very important to make sure which input is currently being used when you are analyzing a recursive function.