Merge Sort for Doubly Linked List

Last Updated on July 24, 2023 by Mayank Dham

Merge sort is a popular and efficient sorting algorithm known for its divide-and-conquer approach. It divides the input array into smaller subarrays, sorts them individually, and then merges the sorted subarrays to produce the final sorted array. While it is widely used in arrays and singly linked lists, its application to doubly linked lists brings forth a unique set of challenges and opportunities. Merging the power of merge sort with the bidirectional traversal capabilities of doubly linked lists offers developers a robust and elegant solution for sorting data efficiently.

In this article, we embark on a journey to explore the intricacies of Merge Sort on Doubly Linked Lists. We delve into the fundamental concepts of merge sort for doubly linked list and also the key features that differentiate doubly linked lists from their singly linked counterparts. As we proceed, we unravel the step-by-step process of adapting the merge sort algorithm to harness the full potential of bidirectional structures.
Let’s understand how to perform merge sort on doubly linked list.

How To Merge Sort on Doubly Linked List?

Merge sort for doubly linked list is quite a complex situation as we compared it with merge sort for array or singly linked list as in doubly linked list, due to its bidirectional feature for traversing in both front and back direction.
Doubly Linked list is having the power to traverse the nodes in forward as well as reverse direction but this power makes things complicated as for now, we have to perform merge sort for doubly linked list.

What is Merge Sort on Doubly Linked List?

In this problem, we will be given a doubly linked list, and we will have to sort the doubly linked list using Merge Sort.

Let’s suppose the given linked list is:

Now using the merge sort we will sort it to obtain the final sorted linked list:

Merge sort is basically a divide and conquer technique in which, we recursively divide the list into two sub-lists at each step till list size is reduced to one and while backtracking from the recursive call, we have two sorted lists which will be merged together by merge() function in linear time.

The above approach is common to both singly-linked lists and doubly-linked lists. The only difference is that we also have to modify the previous pointer while merging the sorted lists. While merging the doubly linked lists, we have to make sure that the previous pointer points to the previously appended node in the merged list.

Now I think from the above example and explanation it is clear what we have to do in the problem as well as what merge sort is.

Now we will look at approach and algorithm to apply merge sort on doubly linked list.

Approach and Algorithm for applying merge sort on doubly linked list

• Find the middle node.
• Split the list around the middle node.
• Recursively call mergeSort on both sub-lists.
• Merge both sorted sub-lists.

Finding middle node of the list

1. We will maintain a fast pointer and a slow pointer. Initially, both pointers will point to the head of the linked list.
2. Now, we will move the slow pointer by one node and the fast pointer by two nodes at a time.
3. When the fast pointer reaches the end of the list, the slow pointer will point to the middle node. So, we will return slowly.

Merging two sorted linked lists

We will use the merge() function to merge the sorted lists. This function accepts two nodes as parameters, list1(node of the first list) and list2(node of the second list).

• If list1 is null, return list2.
• If list2 is null, return list1.
• If list1 is less than list2 append list1 to the resultant list, else append list2.

Dry Run

Let’s try to visualize it (Visualizing Merge Sort):

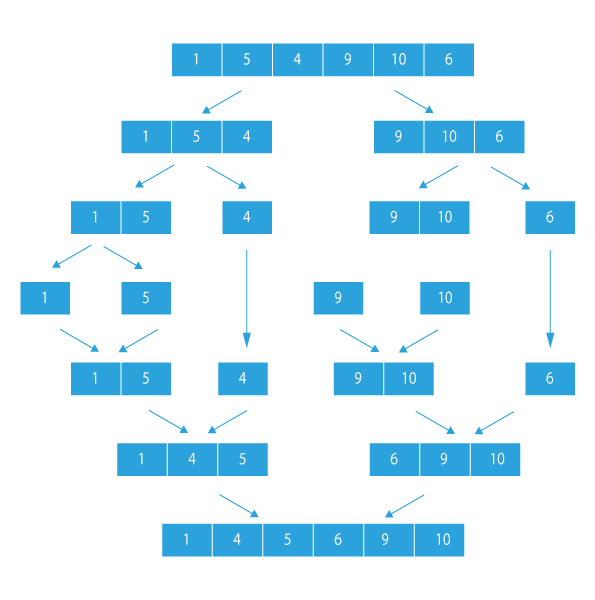
Code Implementation

public class Prepbytes {
    static class Node {
        int data;
        Node next;
        Node prev;

        Node() {
        };

        Node(int num) {
            data = num;
            next = null;
            prev = null;
        }
    };

    public static Node sort(Node head) {
        if (head == null) {
            return head;
        }
       if (head.next == null){
            return head;
        }

        head = mergeSort(head);
        return head;
    }

    public static Node mergeSort(Node dnode) {
        if (dnode == null || dnode.next == null) {
            return dnode;
        }

        Node mid = getMidNode(dnode);
        Node next = mid.next;
        mid.next = null;

        Node l1 = mergeSort(dnode);
        Node l2 = mergeSort(next);

        return merge(l1, l2);
    }

    public static Node merge(Node list1, Node list2) {
        if (list1 == null) {
            return list2;
        }
        if (list2 == null) {
            return list1;
        }
        if (list1.data <= list2.data) {
            list1.next = merge(list1.next, list2);
            list1.next.prev = list1;
            list1.prev = null;
            return list1;
        } else {
            list2.next = merge(list1, list2.next);
            list2.next.prev = list2;
            list2.prev = null;
            return list2;
        }
    }

    public static Node getMidNode(Node node) {
        Node slow = node;
        Node fast = node;
        while (fast.next != null && fast.next.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }

    public static void main(String[] args) {
        Node head = new Node(1);
        head.next = new Node(5);
        head.next.next = new Node(4);
        head.next.next.next = new Node(9);
        head.next.next.next.next = new Node(10);
        head.next.next.next.next.next = new Node(6);

        head = sort(head);
        while (head != null) {
            System.out.print(head.data + " ");
            head = head.next;
        }
    }
}

Output

1 4 5 6 9 10

Time Complexity: O(n*log(n)), where n is the number of nodes in the linked list. The merge sort divides the list into two sub-list and the two sub-lists are merged in linear time.

Conclusion
In conclusion, Merge Sort on a Doubly Linked List presents an elegant and efficient solution for sorting bidirectional data structures. By adapting the classic Merge Sort algorithm to the unique properties of doubly linked lists, developers gain a powerful tool for sorting large datasets while maintaining bidirectional traversal capabilities.

Throughout this article, we explored the step-by-step process of merging a doubly linked list and demonstrated how the algorithm ensures a time complexity of O(N log N) in the worst case. By leveraging the recursive divide-and-conquer approach and intelligently rearranging nodes during merging, Merge Sort on a Doubly Linked List optimizes sorting operations, making it a valuable addition to a developer’s toolkit.

FAQ on Merge Sort for Doubly Linked List

Here are few FAQs related to merge sort on doubly linked list.
Q1. Can Merge Sort be applied to a doubly linked list with a large number of elements?
Absolutely! Merge Sort is known for its efficient time complexity of O(N log N) in the worst case, making it well-suited for sorting doubly linked lists with a large number of elements. The divide-and-conquer approach ensures efficient sorting, even for extensive datasets.

Q2. How does Merge Sort on a Doubly Linked List handle duplicate elements?
Merge Sort is a stable sorting algorithm, meaning it maintains the relative order of elements with equal values during the merging process. Therefore, it preserves the order of duplicate elements, ensuring the doubly linked list remains unchanged if duplicates exist.

Q3. Is it possible to sort a doubly linked list in descending order using Merge Sort?
Yes, Merge Sort on a Doubly Linked List can be adapted to sort the list in descending order. By modifying the comparison condition during the merging step, the algorithm can rearrange elements in descending order instead of ascending.

Q4. Can Merge Sort on a Doubly Linked List handle circular doubly linked lists?
Merge Sort can be adapted to handle circular doubly linked lists. However, special care must be taken to identify the ending condition for splitting the list and breaking the circular reference during merging.

Q5. How does Merge Sort on a Doubly Linked List compare to other sorting algorithms?
Merge Sort offers a stable and efficient solution for sorting doubly linked lists with a time complexity of O(N log N). Compared to other sorting algorithms, it excels in maintaining the bidirectional structure of the list and is particularly well-suited for linked lists where random access is expensive.