In this blog, we tackle a coding task that involves iterative selection sort for linked list. A linked list is unidirectional i.e. we can only traverse the linked list in one direction. A selection sort is an effective sorting algorithm that is used in comparison operations. Let’s understand a brief explanation of the selection sort for linked list.
Problem Statement
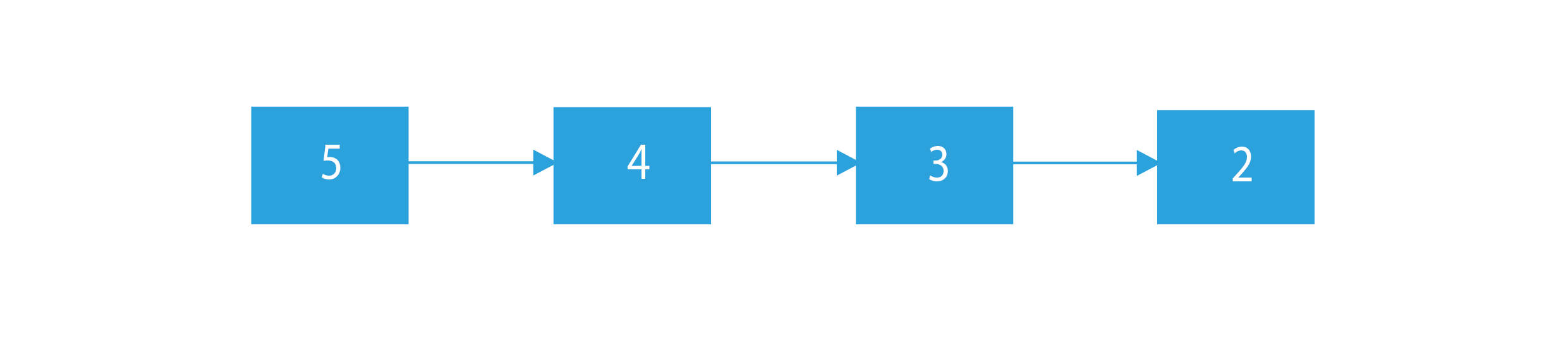
In this problem we are given the head of a linked list denoting the whole linked list, we have to apply the Iterative selection sort for linked list. Suppose we have a linked list represented as –
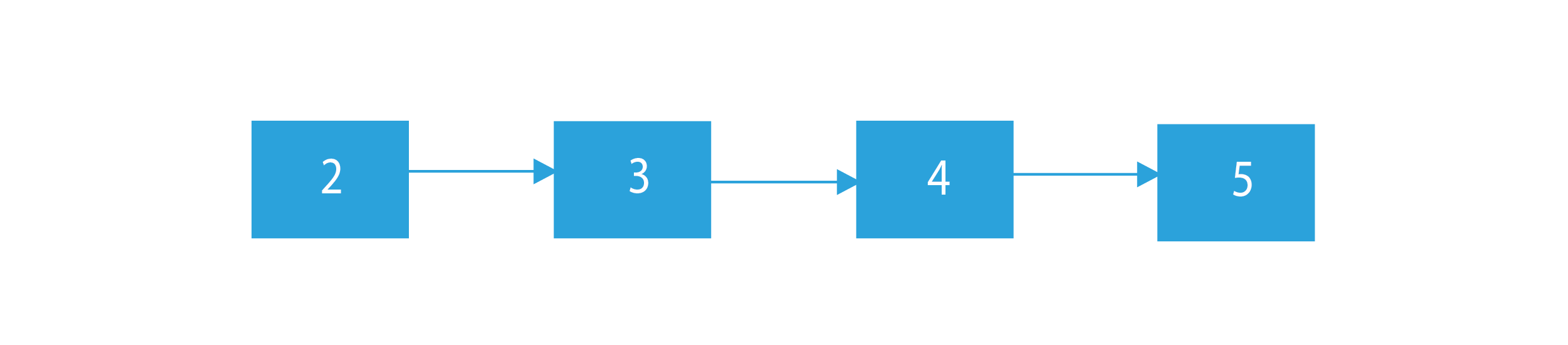
Then the sorted linked list is given as –
Selection sort on the Linked list works in a similar way as it does on arrays but here instead of accessing the elements directly, we will be dealing with the links. Most of the Linked List problems are based on the manipulation of the links.
Approach & Algorithm of Iterative Selection Sort For Linked List
The idea is to Iterate over the given Linked list N times where N is the number of elements in the Linked list. In every iteration of the algorithm, the minimum element (considering ascending order) from the unsorted subarray is picked and moved to the sorted subarray of the Linked list.
Now we have to perform a similar swapping operation, which is done in the Linked list in 2 ways –
- By swapping the data parts of the nodes.
- By swapping the complete nodes.
We will be using here the second way to swap the nodes by manipulating the links. While we do the swapping of the link parts of two nodes, four cases arise:
- When nodes are adjacent and the first node is the head node.
- Nodes can be adjacent and the first node isn’t the head node.
- Nodes might not be adjacent and the first node is the head node.
- Nodes might not be adjacent and the first node isn’t the head node.
Iterative Selection Sort For Linked List Implementation
Iterative Selection Sort For Linked List
#includeusing namespace std; struct Node { int data; Node* next; }; Node* newNode(int val) { Node* temp = new Node; temp->data = val; temp->next = NULL; return temp; } Node* selectionsortfunction(Node* head) { Node *x, *y, *z, *w, *s; x = y = head; while (y->next) { z = w = y->next; while (w) { if (y->data > w->data) { if (y->next == w) { if (y == head) { y->next = w->next; w->next = y; s = y; y = w; w = s; z = w; head = y; w = w->next; } else { y->next = w->next; w->next = y; x->next = w; s = y; y = w; w = s; z = w; w = w->next; } } else { if (y == head) { s = y->next; y->next = w->next; w->next = s; z->next = y; s = y; y = w; w = s; z = w; w = w->next; head = y; } else { s = y->next; y->next = w->next; w->next = s; z->next = y; x->next = w; s = y; y = w; w = s; z = w; w = w->next; } } } else { z = w; w = w->next; } } x = y; y = y->next; } return head; } void show(Node* head) { while (head) { cout << head->data << "->"; head = head->next; } } int main() { Node* head = newNode(5); head->next = newNode(4); head->next->next = newNode(3); head->next->next->next = newNode(2); head = selectionsortfunction(head); show(head); return 0; }
#include#include struct Node { int data; struct Node* next; }; struct Node* newNode(int val) { struct Node* temp = (struct Node*)malloc(sizeof(struct Node)); temp->data = val; temp->next = NULL; return temp; } struct Node* selectionsortfunction(struct Node* head) { struct Node *x, *y, *z, *w, *s; x = y = head; while (y->next) { z = w = y->next; while (w) { if (y->data > w->data) { if (y->next == w) { if (y == head) { y->next = w->next; w->next = y; s = y; y = w; w = s; z = w; head = y; w = w->next; } else { y->next = w->next; w->next = y; x->next = w; s = y; y = w; w = s; z = w; w = w->next; } } else { if (y == head) { s = y->next; y->next = w->next; w->next = s; z->next = y; s = y; y = w; w = s; z = w; w = w->next; head = y; } else { s = y->next; y->next = w->next; w->next = s; z->next = y; x->next = w; s = y; y = w; w = s; z = w; w = w->next; } } } else { z = w; w = w->next; } } x = y; y = y->next; } return head; } void show(struct Node* head) { while (head) { printf("%d->",head->data); head = head->next; } } int main() { struct Node* head = newNode(5); head->next = newNode(4); head->next->next = newNode(3); head->next->next->next = newNode(2); head = selectionsortfunction(head); show(head); return 0; }
class IterativeSort
{
static class Node
{
int data;
Node next;
};
static Node newNode(int val)
{
Node temp = new Node();
temp.data = val;
temp.next = null;
return temp;
}
/* Function to sort a linked list using selection
sort algorithm by swapping the next pointers */
static Node selectionSort(Node head)
{
Node a, b, c, d, r;
a = b = head;
// While b is not the last node
while (b.next != null)
{
c = d = b.next;
// While d is pointing to a valid node
while (d != null)
{
if (b.data > d.data)
{
// If d appears immediately after b
if (b.next == d)
{
if (b == head)
{
b.next = d.next;
d.next = b;
// Swap b and d pointers
r = b;
b = d;
d = r;
c = d;
// Update the head
head = b;
d = d.next;
}
// Case 2: b is not the head of the linked list
else
{
b.next = d.next;
d.next = b;
a.next = d;
// Swap b and d pointers
r = b;
b = d;
d = r;
c = d;
d = d.next;
}
}
/* If b and d have some non-zero number of nodes in between them */
else
{
// Case 3: b is the head of the linked list
if (b == head)
{
// Swap b.next and d.next
r = b.next;
b.next = d.next;
d.next = r;
c.next = b;
// Swap b and d pointers
r = b;
b = d;
d = r;
c = d;
// Skip to the next element
// as it is already in order
d = d.next;
// Update the head
head = b;
}
// Case 4: b is not the head of the linked list
else
{
// Swap b.next and d.next
r = b.next;
b.next = d.next;
d.next = r;
c.next = b;
a.next = d;
// Swap b and d pointers
r = b;
b = d;
d = r;
c = d;
// Skip to the next element
// as it is already in order
d = d.next;
}
}
}
else
{
c = d;
d = d.next;
}
}
a = b;
b = b.next;
}
return head;
}
static void printList(Node head)
{
while (head != null) {
System.out.print(head.data + " ");
head = head.next;
}
}
// Driver Code
public static void main(String args[])
{
Node head = newNode(5);
head.next = newNode(1);
head.next.next = newNode(9);
head = selectionSort(head);
printList(head);
}
}
class Node: def __init__(self, val): self.data = val self.next = None def selectionSort(head): a = b = head while b.next: c = d = b.next while d: if b.data > d.data: if b.next == d: if b == head: b.next = d.next d.next = b b, d = d, b c = d head = b d = d.next else: b.next = d.next d.next = b a.next = d b, d = d, b c = d d = d.next else: if b == head: r = b.next b.next = d.next d.next = r c.next = b b, d = d, b c = d d = d.next head = b else: r = b.next b.next = d.next d.next = r c.next = b a.next = d b, d = d, b c = d d = d.next else: c = d d = d.next a = b b = b.next return head def printList(head): while head: print(head.data, end = " ") head = head.next if __name__ == "__main__": head = Node(5) head.next = Node(4) head.next.next = Node(3) head.next.next.next = Node(2) head = selectionSort(head) printList(head)
Output:
2->3->4->5
Time Complexity for selection sort for linked list : O(N2), where N is the number of nodes present in the Linked List.
Conclusion
In this article, we have tried to explain the selection sort linked list in an iterative fashion and also described its approach and time & space complexities. We hope this article will help you to enhance your knowledge regarding the linked list. You can practice more such problems on the linked list you can check out PrepBytes – Linked List
FAQs regarding selection sort for linked list
- What is meant by selection sort?
- What is the time and space complexity of the selection sort?
- Which sorting is best for the linked list?
- Can we implement selection sort for linked list recursively?
Selection sort is an effective sorting algorithm that is based on comparison operations. Selection sort adds one element in every iteration and selects the smallest element and moves it to the beginning by swapping with the front element.
The time complexity of the selection sort algorithm is O(N2) and the space complexity of O(1).
Merge sort is preferred for sorting a linked list.
Yes, we can implement selection sort for linked list recursively.