The algorithm to insert a node in the middle of a linked list will be covered in this article. One of the key ideas in a linked list is insertion, since it involves dealing with links and changing them as necessary. Let’s attempt to come up with the reasoning behind the method that will insert in middle of linked list.So let’s dive into the article and learn various algorithm to insert a node in the middle of a linked list.
How to Insert an Element in the Middle of a Linked List
We are given a singly linked list and the value x in this problem. The center of the list must have a node with the value x.
With the aid of examples, let’s study programming online and attempt to comprehend the technique for inserting a node in the center of a linked list.
Suppose the given linked list is:
- So now, according to the problem statement, we have to insert a node with value x = 4 into the middle of the list such that our resultant linked list will look like:
Explanation: Here, the current middle of the list is the node with the value 2, so 4 will be inserted just after 2.
If the given linked list is 1 → 3 → 5 → 7 → 9 → 11 and x = 6.
- For the above-linked list, the node with the value 5 is in the middle of the linked list so the node with value x = 6 will be inserted just after the node with the value 5 and our resultant linked list will look like: 1 → 3 → 5 → 6 → 7 → 9 → 11
Explanation: Here, the current middle of the list is the node with value 5, so 6 will be inserted just after 5.
I hope from the above examples the problem is clear, and now the main question is how we should approach the algorithm to insert an element in the middle of a linked list. What is the first thing that comes to mind?
- Finding out the length of the list and then adding the new node just after the (length/2)th node if the length is even, else just after the ((length+1)/2)th node if the length is odd.
- Well, this will be our approach for the algorithm to insert an element in the middle of a linked list. Then afterward, we will see whether we can optimize it or not.
Let us have a glance at the approaches and see where we can optimize the first approach.
Approach for the Algorithm to Insert a Node at the Middle of Linked List (Using the length)
In this approach:
- We will first find the length of the linked list i.e., the number of nodes in the linked list.
- As we know if the length is even, then the middle node is (length/2)th node, else the middle is ((length+1)/2)th node.
- So, if the length is even, we will add the new node after (length/2)th node of the linked list, else we will add the new node after ((length+1)/2)th node of the linked list.
Algorithm to Insert a Node at the Middle of Linked List
- With the help of list traversal, find the length of the linked list. Let the length be len.
- Now, create a variable k. k will (len/2) if len is even, else it will (len+1)/2.
- Here, k denotes the middle point of the list.
- Traverse k nodes and add the new node just after the kth node.
- In this way, the new node gets added into the middle of the list.
This approach is okay, but can we further optimize it?
- If we think carefully, the answer is yes. We can optimize the algorithm to insert an element in the middle of a linked list, as in this technique, we are doing two traversals of the given list.
What if we start by taking two pointers, say slow and fast, and make both points to the head initially.
- What will happen if we make the slow jump one place and the fast jump two places?
- If we notice carefully, by doing the above step when the fast will reach the end of the list, the slow will be pointing to the middle of the list.
- With the help of this technique, we can reach the middle node of a linked list in a single pass.
Note: The reason why slow will be pointing to the middle of the linked list when fast reaches the end is that, as our slow pointer is travelling with half of the speed of the fast pointer, so when fast pointer will reach the end of the linked list, till that time slow pointer will have travelled only half the distance as travelled by fast pointer and hence it will be at the middle of the linked list.
Do you know what the above-explained method is called?
- This method is called the tortoise and hare method or the slow and fast pointer method.
The slow and fast pointer method has been explained in detail in the approach section and the dry run.
Approach to insert node at middle of linked list (Slow and Fast Pointer)
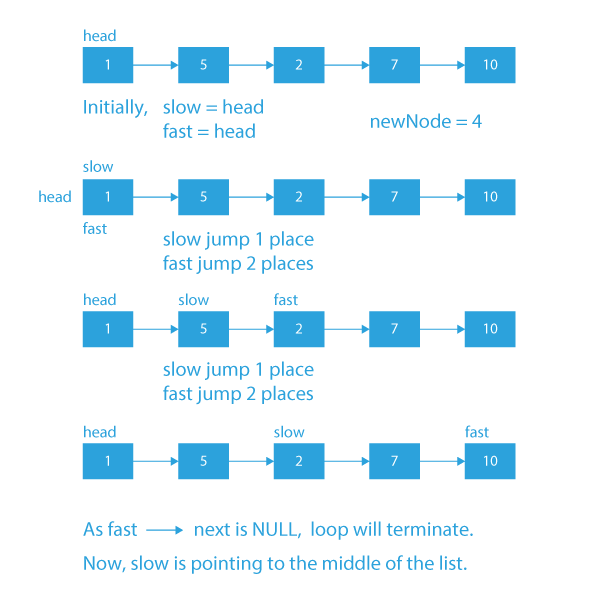
Let us see what the slow and fast pointer technique is:
- Initially, both the pointers, slow and fast, will point to the head of the linked list.
- Then, we will start moving both of the pointers. The fast pointer will jump two places, whereas the slow pointer will jump only one place.
- When the fast pointer reaches the end of the linked list, the slow pointer will be pointing to the middle of the linked list.
- Now, as we have the slow pointer pointing to the middle of the list, we will add the new node just after the slow pointer.
Algorithm to Insert Node at Middle of Linked List
- Create two-pointer slow and fast. Both slow and fast will be pointing to the head of the list.
- Now, the slow will jump one place and the fast will jump two places.
- When the fast pointer reaches the end of the list, the slow will be pointing to the middle of the list.
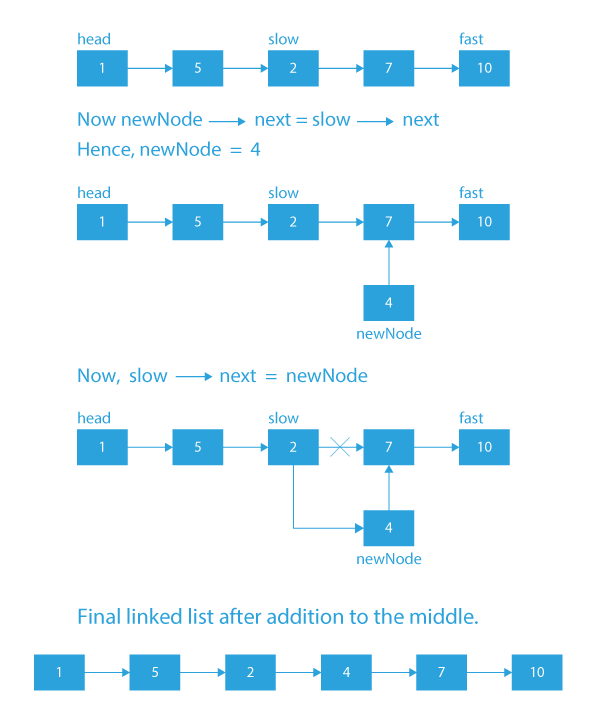
- Add the new node newNode just after the slow pointer following the below steps.
- newNode – > next = slow – > next
- slow – > next = newNode
- Finally, our newNode will be inserted into the middle of the linked list and our objective will be achieved.
DRY RUN of the Algorithm to Insert a Node at the Middle of Linked List
Code Implementation of the Algorithm to Insert a Node at the Middle of Linked List
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
// function to create and return a node
struct Node* getNode(int data)
{
// allocating space
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// inserting the required data
newNode->data = data;
newNode->next = NULL;
return newNode;
}
// function to insert node at the middle
// of the linked list
void insertAtMid(struct Node** head_ref, int x)
{
// if list is empty
if (*head_ref == NULL)
*head_ref = getNode(x);
else {
// get a new node
struct Node* newNode = getNode(x);
struct Node* ptr = *head_ref;
int len = 0;
// calculate length of the linked list
//, i.e, the number of nodes
while (ptr != NULL) {
len++;
ptr = ptr->next;
}
// 'count' the number of nodes after which
// the new node is to be inserted
int count = ((len % 2) == 0) ? (len / 2) :
(len + 1) / 2;
ptr = *head_ref;
// 'ptr' points to the node after which
// the new node is to be inserted
while (count-- > 1)
ptr = ptr->next;
// insert the 'newNode' and adjust the
// required links
newNode->next = ptr->next;
ptr->next = newNode;
}
}
// function to display the linked list
void display(struct Node* head)
{
while (head != NULL) {
printf("%d ",head->data);
head = head->next;
}
}
// Driver program to test above
int main()
{
// Creating the list 1->2->4->5
struct Node* head = NULL;
head = getNode(1);
head->next = getNode(2);
head->next->next = getNode(4);
head->next->next->next = getNode(5);
printf("Linked list before insertion: ");
display(head);
int x = 3;
insertAtMid(&head, x);
printf("\nLinked list after insertion: ");
display(head);
return 0;
}
#include <bits stdc++.h="">
using namespace std;
struct Node {
int data;
Node* next;
};
Node* getNode(int data)
{
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->data = data;
newNode->next = NULL;
return newNode;
}
void insertAtMid(Node** head_ref, int x)
{
if (*head_ref == NULL)
*head_ref = getNode(x);
else {
Node* newNode = getNode(x);
Node* slow = *head_ref;
Node* fast = *head_ref;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
}
newNode->next = slow->next;
slow->next = newNode;
}
}
void display(Node* head)
{
while (head != NULL) {
cout << head->data << " ";
head = head->next;
}
}
int main()
{
Node* head = NULL;
head = getNode(1);
head->next = getNode(5);
head->next->next = getNode(2);
head->next->next->next = getNode(7);
head->next->next->next->next = getNode(10);
cout << "Linked list before insertion: ";
display(head);
int x = 4;
insertAtMid(&head, x);
cout << "\nLinked list after insertion: ";
display(head);
return 0;
}
import java.util.*;
import java.lang.*;
import java.io.*;
public class LinkedList
{
static Node head;
static class Node {
int data;
Node next;
Node(int d) {
data = d;
next = null;
}
}
static void insertAtMid(int x)
{
if (head == null)
head = new Node(x);
else {
Node newNode = new Node(x);
Node slow = head;
Node fast = head;
while (fast != null && fast.next
!= null)
{
slow = slow.next;
fast = fast.next.next;
}
newNode.next = slow.next;
slow.next = newNode;
}
}
static void display()
{
Node temp = head;
while (temp != null)
{
System.out.print(temp.data + " ");
temp = temp.next;
}
}
public static void main (String[] args)
{
head = null;
head = new Node(1);
head.next = new Node(5);
head.next.next = new Node(2);
head.next.next.next = new Node(7);
head.next.next.next.next = new Node(10);
System.out.println("Linked list before insertion: ");
display();
int x = 4;
insertAtMid(x);
System.out.println("\nLinked list after insertion: ");
display();
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
def insertAtMid(head, x):
if(head == None):
head = Node(x)
else:
newNode = Node(x)
ptr = head
length = 0
while(ptr != None):
ptr = ptr.next
length += 1
if(length % 2 == 0):
count = length / 2
else:
count = (length + 1) / 2
ptr = head
while(count > 1):
count -= 1
ptr = ptr.next
newNode.next = ptr.next
ptr.next = newNode
def display(head):
temp = head
while(temp != None):
print(str(temp.data), end = " ")
temp = temp.next
head = Node(1)
head.next = Node(5)
head.next.next = Node(2)
head.next.next.next = Node(7)
head.next.next.next.next = Node(10)
print("Linked list before insertion: ", end = "")
display(head)
x = 4
insertAtMid(head, x)
print("\nLinked list after insertion: " , end = "")
display(head)
Output
Linked list before insertion: 1 5 2 7 10
Linked list after insertion: 1 5 2 4 7 10Space Complexity: O(1), as only temporary variables are being created.
Conclusion
Finding the middle node and adjusting the pointers to incorporate the new node are the two most important steps in inserting a node into the middle of a linked list. We can insert a node into the middle of the linked list without disrupting the existing structure by correctly manipulating the pointers. This operation is commonly used in a variety of applications where an ordered or sorted linked list must be maintained.
Frequently Asked Questions (FAQs)
Q1: What is a linked list?
Ans. A linked list is a linear data structure where elements are stored in nodes. Each node contains a data element and a pointer that points to the next node in the list. It allows for dynamic memory allocation and efficient insertion and deletion operations.
Q2: How do I insert a node into the middle of a linked list?
Ans. To insert a node into the middle of a linked list, follow these steps:
- Find the middle node using the slow and fast pointer technique.
- Create a new node with the desired data.
- Adjust the pointers of the previous node and the new node to incorporate the new node.
- Update the pointers of the new node and the next node to maintain the list’s connectivity.
Q3: What is the time complexity of inserting a node into the middle of a linked list?
Ans. The time complexity of inserting a node into the middle of a linked list is O(n), where n is the number of nodes in the list. This is because finding the middle node requires traversing the list, which takes linear time. Once the middle node is found, the actual insertion operation takes constant time.
Q4: Can I insert a node into the middle of a singly linked list?
Ans. Yes, you can insert a node into the middle of a singly linked list. The process involves finding the middle node using the slow and fast pointer technique and adjusting the pointers accordingly.
Q5: What happens if the linked list has an even number of nodes?
Ans. If the linked list has an even number of nodes, there are two possible middle nodes. In such cases, you can choose to insert the new node either before or after the exact middle node, depending on your requirements.
Q6: What if the linked list is empty?
Ans. If the linked list is empty, inserting a node into the middle is not possible since there are no nodes, to begin with. In that case, you can consider inserting the node at the head or simply creating a new linked list with the single node.
Q7: Can I insert a node at the beginning or end of a linked list using the same method?
Ans. No, inserting a node at the beginning or end of a linked list requires different steps compared to inserting a node in the middle. For insertion at the beginning, you need to adjust the head pointer. For insertion at the end, you need to traverse the list until you reach the last node and then adjust the pointers accordingly.