Convert a given Binary Tree To Doubly Linked List | Set 3

Last Updated on August 9, 2024 by Abhishek Sharma

Converting a binary tree to a doubly linked list is a common problem in data structures, often asked in coding interviews and competitive programming. The goal is to transform the binary tree structure into a doubly linked list (DLL) while maintaining the in-order traversal sequence of the original tree. This transformation is particularly useful in scenarios where tree-based data needs to be sequentially accessed, like in flattening operations or when creating a linear representation of hierarchical data. This article explores the concept, methodology, and key considerations in converting a binary tree to a doubly linked list.

How to Convert a given Binary Tree To Doubly Linked List

In this problem, we are given a binary tree, and we have to convert it to a doubly linked list.

Problem Statement Understanding

Let’s try to understand the problem statement with the help of examples.

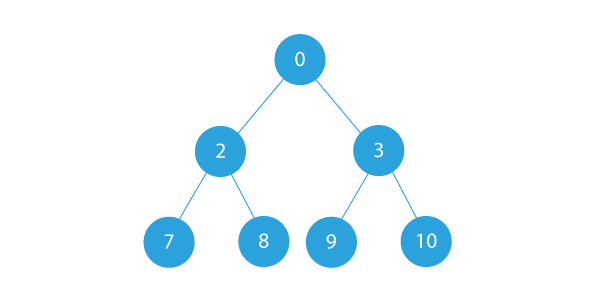
Let’s assume that the given binary tree is:

• According to the problem statement, we need to convert this given binary tree to a doubly linked list.
• After converting the given tree to a doubly linked list, our doubly linked list will look like:

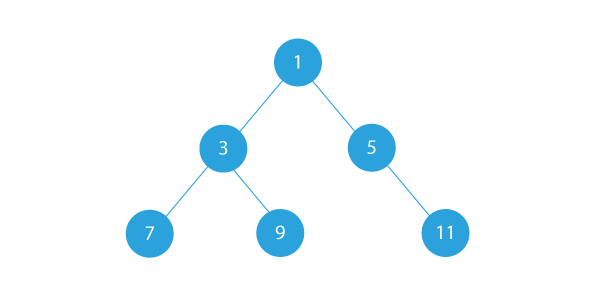
Taking another example, if the given binary tree is:

• Then, in this case, our doubly linked list will be:

Now, I think from the above examples, the problem statement is clear. Let’s see how we can approach it.

Before moving to the approach section, try to think about how you can approach this problem.

• If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.

Before moving on further, let’s see some helpful observations, which will help us to approach this problem.

Helpful Observations

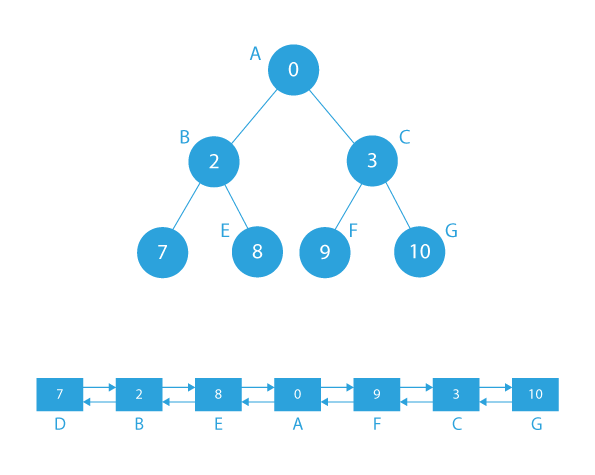
Let’s name every node to check its relative position in the binary tree and doubly linked list.

In the binary tree, we can observe that:

• The root node is A, which has B as its left child and C as its right child.
• B has D as its left child and E as its right child.
• C has F as its left child and G as its right child.

In the converted doubly linked list, we can observe that:

• Node B has D as its previous node, which was its left child in the binary tree, and E as its next node, which was its right child in the binary tree.
• Node C has F as its previous node, which was its left child in the binary tree, and G as its next node, which was its right child in the binary tree.

So, from the above observations, you might think that we can just make the previous pointer of a node point to its left child and the next pointer point to its right child.

• Yes, that is partially true because, as you can see the node A has B as its left child, but its previous pointer is pointing to E in the doubly linked list.

Another observation here is that all the nodes in the left subtree rooted at a node lie on the left side of the node in the list. Similarly, all the nodes in the right subtree rooted at a node lie on the right side of the node in the list.

• We can achieve this using inorder traversal of the tree.

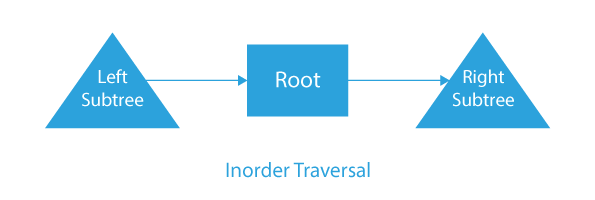
Inorder order traversal: In inorder traversal, we first visit the left subtree, then the root, and then right subtree:

If we do the inorder traversal of the given above given tree, we will get:
7 2 8 0 9 3 10

On careful observation, you can see, the values are in the same order as in our output list.

So, the key takeaways are:

• The left child can only be replaced with the previous node and the right child with the next node.
• The nodes of the doubly linked list should follow the same order as the inorder traversal of the tree.

Approach

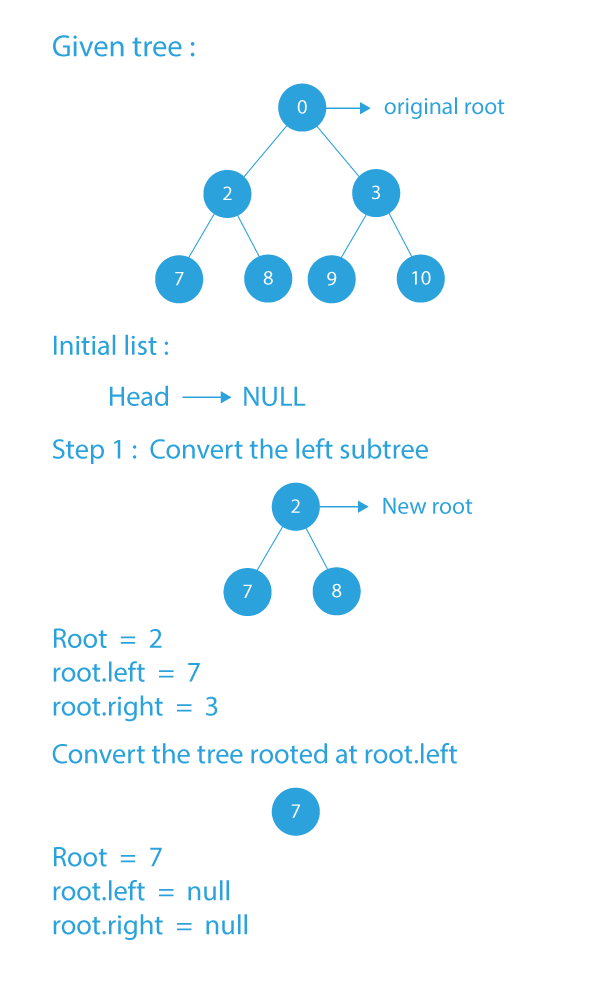
• From the above observations, it is clear that the list will have nodes in the same order as the inorder traversal of the tree. So, we first convert the left subtree to a doubly linked list and append the resultant list to the final list and then append the root node to the final list and then convert the right subtree to a doubly linked list and append the resultant list to the final list.
• Now the question arises, how do we convert the left subtree or the right subtree to a doubly linked list. And the answer is recursion.
• A subtree follows all the properties of the parent tree. So this problem is similar to the original problem. We treat the left child of the root as the new root and convert the subtree rooted at the left child (left child of the left child of the original root) of the new root (left child of the original root) and then convert the new root and then the subtree rooted at the right child of the new root.
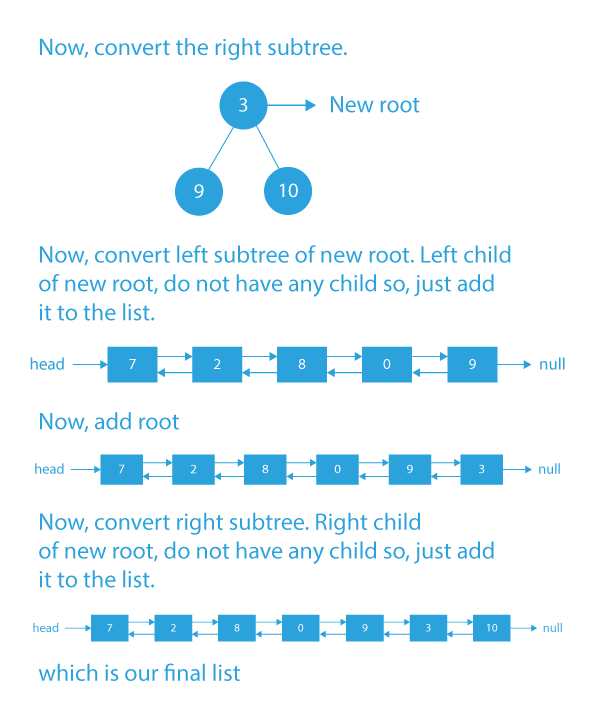
• We perform this operation recursively until the problem becomes trivial to solve. By trivial problem, I mean converting a binary tree that has at most three nodes, a root, left child, and right child. This problem can be solved easily as we just first append the left child to the list, then the root, and then the right child.
• To append a node to the list, we just need to make the next pointer of the head node point to the node, and make the previous pointer of this node point to the head.

Algorithm

To convert the given binary tree to a doubly linked list, we need to do an inorder traversal of the binary tree.

• Create a node Head, which will act as the starting node of our doubly linked list.
• Create a method convertToDoubleLinkedList(), which is called recursively, to perform inorder traversal on the binary tree and convert it to a doubly linked list.
• Call method convertToDoubleLinkedList() on the root.
• If the root is null, that means the tree rooted at this root does not exist. So, we simply return.
• Call the method convertToDoubleLinkedList() on the left child of the root node (the node which is passed to the convertToDoubleLinkedList method). This will convert the left subtree rooted at the root node by recursively calling all the subtrees rooted at the root.left as well as root.right and append the list to the final output list.
• As the left subtree is already converted to the list, append the root node to the list.
• Call the method convertToDoubleLinkedList() on the right child of the root node (the node which is passed to the convertToDoubleLinkedList method). This will convert the right subtree rooted at the root node by recursively calling all the subtrees rooted at the root.left as well as root.right and append the list to the final output list.
• Now, print the final list.

Dry Run

Code Implementation

#include <stdio.h>
#include<stdlib.h>
 
struct node
{
    int data;
    struct node* left;
    struct node* right;
};
 
// A simple recursive function to convert a given Binary tree to Doubly
// Linked List
// root --> Root of Binary Tree
// head --> Pointer to head node of created doubly linked list
void BinaryTree2DoubleLinkedList(struct node *root,struct node **head)
{
    // Base case
    if (root == NULL) return;
 
    // Initialize previously visited node as NULL. This is
    // static so that the same value is accessible in all recursive
    // calls
    static struct node* prev = NULL;
 
    // Recursively convert left subtree
    BinaryTree2DoubleLinkedList(root->left, head);
 
    // Now convert this node
    if (prev == NULL)
        *head = root;
    else
    {
        root->left = prev;
        prev->right = root;
    }
    prev = root;
 
    // Finally convert right subtree
    BinaryTree2DoubleLinkedList(root->right, head);
}
 
/* Helper function that allocates a new node with the
   given data and NULL left and right pointers. */
struct node* newNode(int data)
{
     struct node* new_node = (struct node*)malloc(sizeof(struct node));
    new_node->data = data;
    new_node->left = new_node->right = NULL;
    return (new_node);
}
 
/* Function to print nodes in a given doubly linked list */
void printList(struct node *node)
{
    while (node!=NULL)
    {
        printf("%d ",node->data);
        node = node->right;
    }
}
 
/* Driver program to test above functions*/
int main()
{
    // Let us create the tree shown in above diagram
    struct node *root        = newNode(10);
    root->left        = newNode(12);
    root->right       = newNode(15);
    root->left->left  = newNode(25);
    root->left->right = newNode(30);
    root->right->left = newNode(36);
 
    // Convert to DLL
    struct node *head = NULL;
    BinaryTree2DoubleLinkedList(root, &head);
 
    // Print the converted list
    printList(head);
 
    return 0;
}

#include <iostream>
using namespace std;
 
/* A binary tree node has data, and left and right pointers */
struct node
{
    int data;
    node* left;
    node* right;
};
 
// A simple recursive function to convert a given Binary tree to Doubly
// Linked List
// root --> Root of Binary Tree
// head --> Pointer to head node of created doubly linked list
void BinaryTree2DoubleLinkedList(node *root, node **head)
{
    // Base case
    if (root == NULL) return;
 
    // Initialize previously visited node as NULL. This is
    // static so that the same value is accessible in all recursive
    // calls
    static node* prev = NULL;
 
    // Recursively convert left subtree
    BinaryTree2DoubleLinkedList(root->left, head);
 
    // Now convert this node
    if (prev == NULL)
        *head = root;
    else
    {
        root->left = prev;
        prev->right = root;
    }
    prev = root;
 
    // Finally convert right subtree
    BinaryTree2DoubleLinkedList(root->right, head);
}
 
/* Helper function that allocates a new node with the
   given data and NULL left and right pointers. */
node* newNode(int data)
{
    node* new_node = new node;
    new_node->data = data;
    new_node->left = new_node->right = NULL;
    return (new_node);
}
 
/* Function to print nodes in a given doubly linked list */
void printList(node *node)
{
    while (node!=NULL)
    {
        cout << node->data << " ";
        node = node->right;
    }
}
 
/* Driver program to test above functions*/
int main()
{
    // Let us create the tree shown in above diagram
    node *root        = newNode(10);
    root->left        = newNode(12);
    root->right       = newNode(15);
    root->left->left  = newNode(25);
    root->left->right = newNode(30);
    root->right->left = newNode(36);
 
    // Convert to DLL
    node *head = NULL;
    BinaryTree2DoubleLinkedList(root, &head);
 
    // Print the converted list
    printList(head);
 
    return 0;
}

public class Prepbytes
{
    // Structure of a tree node
    static class Node
    {
        int data;
        Node left = null;
        Node right = null;
     
        Node(int data) {
            this.data = data;
        }
    }

    static Node head;
    static Node prev = null;

    // Using this function we will be converting a tree rooted at this node to a doubly linked list.
    static void convertToDoubleLinkedList(Node root)
    {
        if (root == null)
            return;
  
    
        convertToDoubleLinkedList(root.left);
  
    
        if (prev == null)
            head = root;
        else
        {
            root.left = prev;
            prev.right = root;
        }
        prev = root;
  
        convertToDoubleLinkedList(root.right);
    }
    
    
    // Using this function we will be printing the Doubly Linked List.
    public static void printDoublyLinkedList(Node head)
    {
        Node curr = head;
        while (curr != null)
        {
            System.out.print(curr.data + " ");
            curr = curr.right;
        }
    }
 
    public static void main(String[] args)
    {
        Node root = new Node(0);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(7);
        root.left.right = new Node(8);
        root.right.left = new Node(9);
        root.right.right = new Node(10);
 
        convertToDoubleLinkedList(root);
        System.out.println("Converted Doubly linked list");
        printDoublyLinkedList(head);
    }
}

class Node:
    def __init__(self, data):
        self.right = None
        self.data = data
        self.left = None


class BtoDll:
    def __init__(self):
        self.head = None
        self.tail = None

    def convert(self, root):
    
        if root is None:
            return
        
        self.convert(root.left)
        
        node = root
        if self.head is None:
            self.head = node
        else:
            self.tail.right = node
            node.left = self.tail
        self.tail = node
        
        self.convert(root.right)
        return self.head


def BinaryTree2DoubleLinkedList(root):
    converter = BtoDll()
    return converter.convert(root)


def print_dll(head):
    while head is not None:
        print(head.data, end=" ")
        head = head.right


if __name__ == "__main__":

    root = Node(0)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(7)
    root.left.right = Node(8)
    root.right.left = Node(9)
    root.right.right = Node(10)
    
    head = BinaryTree2DoubleLinkedList(root)
    print("Converted Doubly linked list")
    print_dll(head)

Output

Converted Doubly linked list
7 2 8 0 9 3 10

Time Complexity: O(n), where n is the total number of nodes in the given binary tree. To convert the given binary tree to the doubly linked list we traverse the binary tree which takes linear time. It is not possible to solve this problem in time less than linear time because that would mean we do not traverse each node and have missed some nodes.

Space Complexity: O(h), where h is the height of the binary tree. At any instant, the space occupied by the recursive stack is at most h.

Conclusion
Converting a binary tree to a doubly linked list involves a strategic in-order traversal that links nodes in a linear fashion while preserving the original tree’s structure. This operation is useful for various applications, including sequential access and tree flattening, providing an efficient way to handle tree data in a linear format. Understanding this conversion process not only deepens your knowledge of data structures but also enhances your problem-solving skills in coding interviews and practical applications.

FAQs related to Convert a given Binary Tree to Doubly Linked List

Here are some FAQs related to Convert a given Binary Tree to Doubly Linked List:

Q1: What is the significance of converting a binary tree to a doubly linked list?
A1: Converting a binary tree to a doubly linked list is significant for scenarios where sequential access to tree nodes is required. It also simplifies operations like tree traversal and data manipulation by providing a linear structure.

Q2: How does the in-order traversal relate to the conversion process?
A2: The in-order traversal is crucial in this conversion process as it ensures that the doubly linked list maintains the sorted order of the binary tree. Nodes are linked in the exact sequence they would appear in an in-order traversal.

Q3: Can this conversion be done without using extra space?
A3: Yes, this conversion can be performed in-place without using extra space by modifying the tree nodes themselves to serve as the nodes of the doubly linked list.

Q4: What are the time complexity and space complexity of this conversion?
A4: The time complexity of converting a binary tree to a doubly linked list is O(n), where n is the number of nodes in the tree. The space complexity can be O(1) if the conversion is done in-place.

Q5: Is it possible to convert a binary tree to a circular doubly linked list?
A5: Yes, a binary tree can be converted to a circular doubly linked list by linking the last node back to the first node, forming a circular structure that allows for continuous traversal in both directions.