The linked list is one of the most important topics of data structures. In this blog, we have a problem in which we have to construct a 2D linked list. Let’s have a look at the problem statement for a better understanding of the 2D linked list.
How to construct a linked list from a 2D matrix
In this problem, we would be given a 2D matrix, and we need to construct a linked list from it.
Let’s see what the problem is demanding.
- In this problem, we will be given a 2D matrix, and we just need to establish the link between all the elements of the matrix.
- Considering the elements of the matrix as a node of a linked list, we need to connect a node with its immediate right and down elements in the respective matrix.
- If there is no element present to the immediate right or immediate down of an element, then we need to consider the immediate right and down elements as NULL.
Let us try to understand the problem statement with the help of examples.
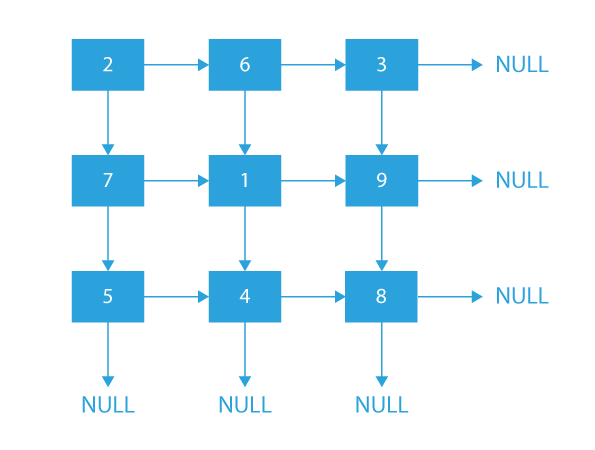
Input
2 6 3
7 1 9
5 4 8
Output
Explanation
- In the above example, all the nodes are connected in the same manner as they are present in the matrix.
- For example, Node 6 is pointing to two different nodes, i.e., its right pointer points to its immediate right element, which is 3 and its down pointer points to its immediate down element which is 1.
- When there are no nodes present to the immediate right or down of an element, i.e., for boundary elements, it is considered as the end of the list, and they are made to point NULL pointer. For example, as there is no right element of 9, so its right pointer is made to point NULL pointer.
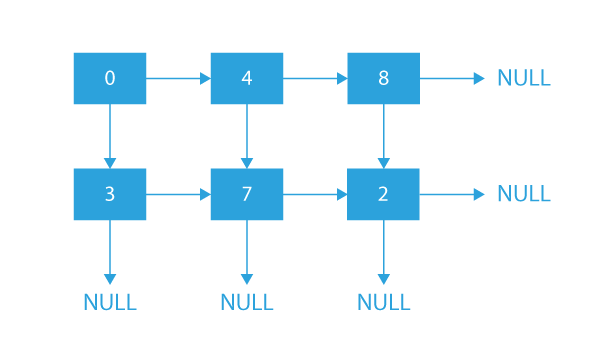
Input
0 4 8
3 7 2
Output
Now, I hope from the above examples the problem is clear. So now, let’s think about how we can approach this problem?
In the next section, have a look at some helpful observations.
Helpful observations
- We need to construct a linked list in which each node will have two pointers named right and down.
- We just need to create a node for each cell of the matrix and then attach it to its right and down elements, respectively.
- Remember to point to a NULL pointer when we reach the boundary of the matrix.
Approach of 2D linked list
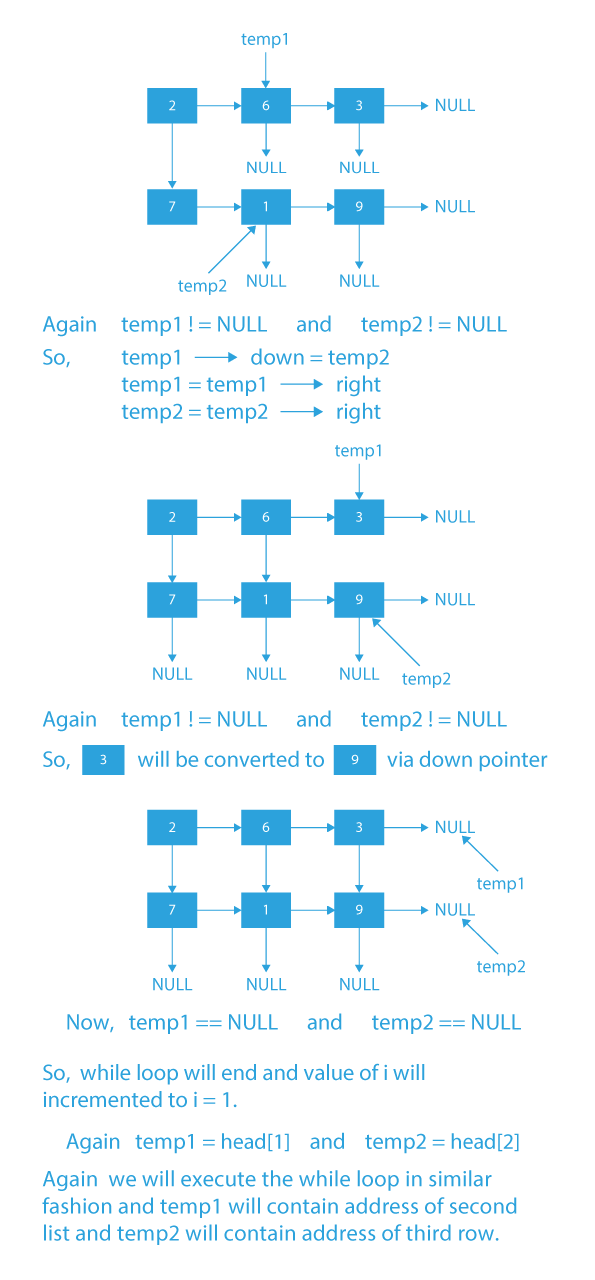
- We will first create N (N = number of rows) linked lists, where ith linked list will contain all the elements of the ith row of the given matrix. Each node of ith linked list will store the address of its immediate right element from the matrix in its right link.
- We will create an array of pointers that will keep track of the address of the first nodes of all N lists that are created in the previous step.
- Then, we will traverse all lists one by one, and while traversing for ith list, we will assign the down pointer of each node to its corresponding immediate down element in (i+1)th list.
Algorithm of 2D linked list
-
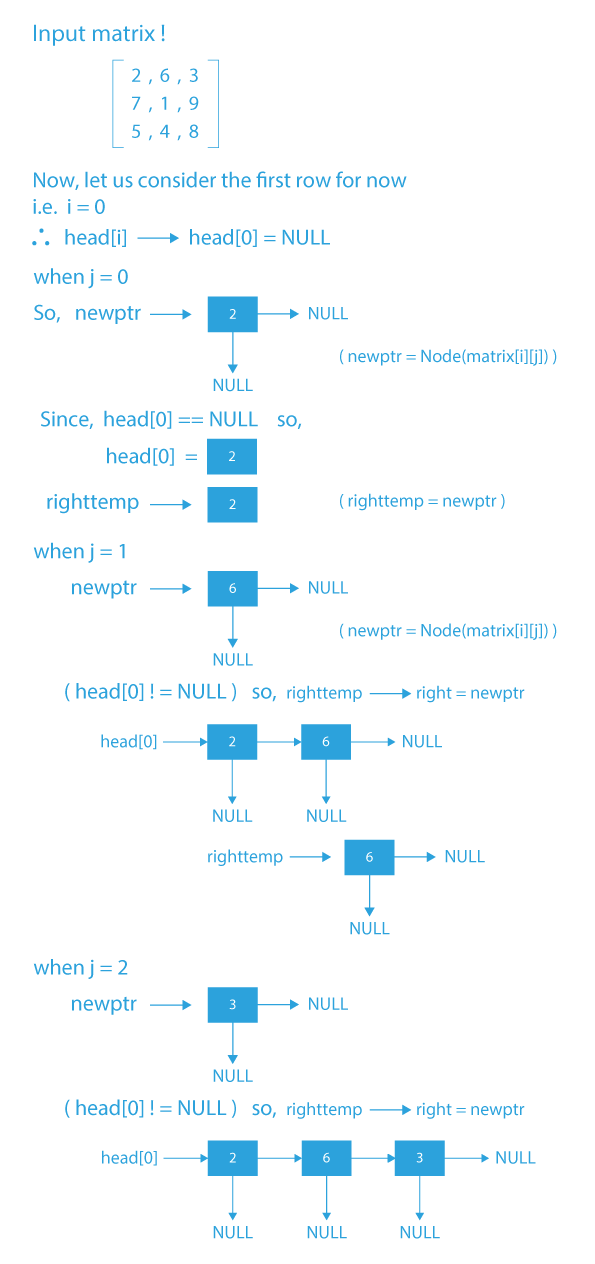
Create an array of pointers (say head) of size equal to the number of rows in the matrix.
-
Create a for loop that will traverse through all the matrix rows and inside this for loop initialize the head[i] to NULL.
-
Create a nested for loop (inner loop of for loop which we created in previous step) to traverse the column elements of the matrix and while traversing create new nodes having value equal to the value at corrsponding position in the original matrix and then, check if head[i] is NULL or not.
- If head[i] is NULL, that means we are at the first column, so we need to store the address of the newly created node into this head[i].
- If head[i] is not NULL, we will attach this current node in the ith linked list.
- Then store the address of this node in the righttemp variable so that we can attach the new node after this node further.
-
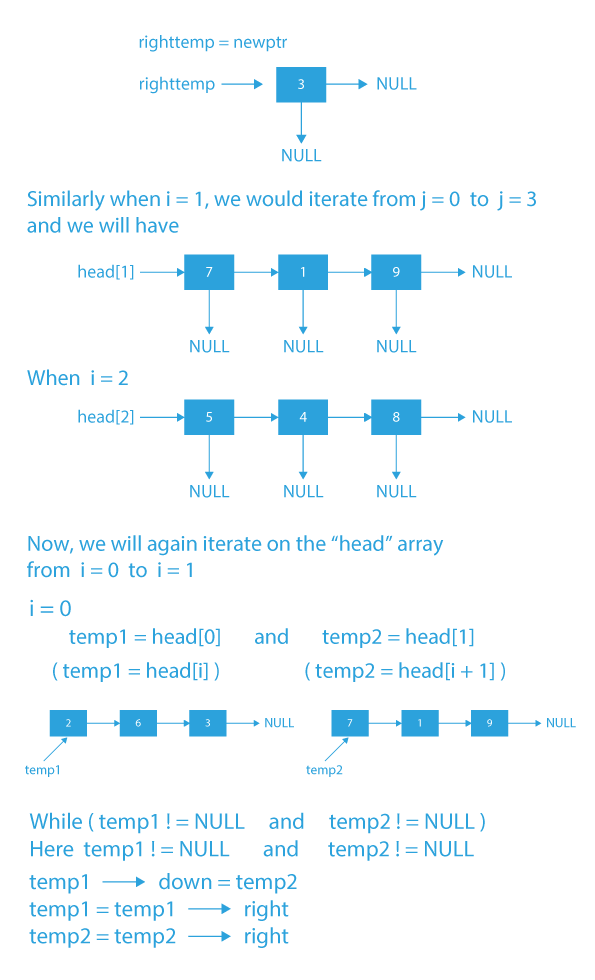
After the execution of the above nested for loops, we need to loop through the head array again and connect down pointers of the corresponding ith list to (i+1)th list.
-
Now return head[0] from the function, as it would contain the address of the first node of the newly created linked list.
-
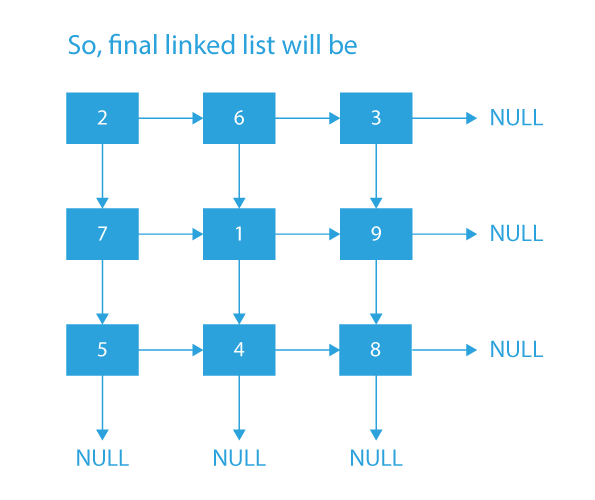
After performing the above steps, we would get our desired linked list constructed from the given 2-D matrix.
Dry Run of 2D linked list
Code Implementation
#include <stdio.h>
#include<stdlib.h>
struct node {
int data;
struct node *right, *down;
};
// utility function to create a new node with given data
struct node* newNode(int d)
{
struct node* temp = (struct node*)malloc(sizeof(struct node));
temp->data = d;
temp->right = temp->down = NULL;
return temp;
}
// utility function to print the linked list pointed to by head pointer
void display(struct node* head)
{
struct node *rp, *dp = head;
// loop until the down pointer is not NULL
while (dp) {
rp = dp;
// loop until the right pointer is not NULL
while (rp) {
printf("%d ",rp->data);
rp = rp->right;
}
printf("\n");
dp = dp->down;
}
}
// function which constructs the linked list
// from the given matrix of size m * n
// and returns the head pointer of the linked list
struct node* constructLinkedMatrix(int mat[][3], int m, int n)
{
// stores the head of the linked list
struct node* mainhead = NULL;
// stores the head of linked lists of each row
struct node* head[m];
struct node *righttemp, *newptr;
// Firstly, we create m linked lists
// by setting all the right nodes of every row
for (int i = 0; i < m; i++) {
// initially set the head of ith row as NULL
head[i] = NULL;
for (int j = 0; j < n; j++) {
newptr = newNode(mat[i][j]);
// stores the mat[0][0] node as
// the mainhead of the linked list
if (!mainhead)
mainhead = newptr;
if (!head[i])
head[i] = newptr;
else
righttemp->right = newptr;
righttemp = newptr;
}
}
// Then, for every ith and (i+1)th list,
// we set the down pointers of
// every node of ith list
// with its corresponding
// node of (i+1)th list
for (int i = 0; i < m - 1; i++) {
struct node *temp1 = head[i], *temp2 = head[i + 1];
while (temp1 && temp2) {
temp1->down = temp2;
temp1 = temp1->right;
temp2 = temp2->right;
}
}
// return the mainhead pointer of the linked list
return mainhead;
}
// Driver program to test the above function
int main()
{
int m, n; // m = rows and n = columns
m = 3, n = 3;
// 2D matrix
int mat[][3] = { { 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 } };
struct node* head = constructLinkedMatrix(mat, m, n);
display(head);
return 0;
}
#includeusing namespace std; class Node { public: int data; Node* right, *down; Node(int x){ data = x; right = NULL; down = NULL; } }; void display(Node* head) { // pointer that will move rightwards Node* Rp; // pointer that will move downwards Node* Dp = head; // iterate till down pointer is not NULL while (Dp) { Rp = Dp; // iterate till right pointer is not NULL while (Rp) { cout << Rp->data << " "; Rp = Rp->right; } cout << "\n"; Dp = Dp->down; } } Node* constructLinkedListMatrix(int mat[][3], int n, int m) { // array to store starting address of each each row Node* head[m]; Node *righttemp, *newptr; // create ‘n’ linked lists for each row for (int i = 0; i < n; i++) { // initialize head[i] with NULL head[i] = NULL; for (int j = 0; j < m; j++) { // create a new node newptr = new Node(mat[i][j]); // this means that we are in first column so we need // to store the address of first node of each row if (!head[i]) head[i] = newptr; else righttemp->right = newptr;// attach node to its // right node righttemp = newptr; } } // For every ith row’s list set corresponding down pointers // to (i+1)th list’s node for (int i = 0; i < n - 1; i++) { Node *temp1 = head[i], *temp2 = head[i + 1]; while (temp1 && temp2) { temp1->down = temp2; temp1 = temp1->right; temp2 = temp2->right; } } // return the head[0] pointer as it is the main head pointer // of the newly created list return head[0]; } int main() { // 2D matrix int arr[][3] = { { 2, 6, 3 }, { 7, 1, 9 }, { 5, 4, 8 } }; int row = 3, col = 3; Node* head = constructLinkedListMatrix(arr, row, col); display(head); return 0; }
class Node
{
int data;
Node right,down;
Node()
{
}
Node(int data)
{
this.data=data;
}
}
public class Matrix
{
static void display(Node head)
{
Node Rp;
Node Dp=head;
while(Dp!=null)
{
Rp=Dp;
while(Rp!=null)
{
System.out.print(Rp.data+" ");
Rp=Rp.right;
}
System.out.println();
Dp=Dp.down;
}
}
static Node constructLinkedMatrix(int[][] arr,int m, int n)
{
// stores the head of the linked list
Node mainHead = null;
// stores the head of linked lists of each row
Node[] head = new Node[m];
Node rightTemp = new Node(), newptr;
// Firstly, we create m linked lists
// by setting all the right nodes of every row
for(int i = 0; i < m; i++)
{
// initially set the head of ith row as NULL
head[i] = null;
for(int j = 0; j < n; j++)
{
newptr = new Node(arr[i][j]);
// stores the mat[0][0] node as the mainhead of the linked list
if(mainHead == null)
mainHead = newptr;
if(head[i] == null)
head[i] = newptr;
else
rightTemp.right = newptr;
rightTemp = newptr;
}
}
// Then, for every ith and (i+1)th list,
// we set the down pointers of every node of ith list
// with its corresponding node of (i+1)th list
for(int i = 0; i < m - 1; i++)
{
Node temp1 = head[i], temp2 = head[i + 1];
while(temp1 != null && temp2 != null)
{
temp1.down = temp2;
temp1 = temp1.right;
temp2 = temp2.right;
}
}
// return the mainhead pointer of the linked list
return mainHead;
}
public static void main(String[] args)
{
int arr[][] = {{ 2, 6, 3 },
{ 7, 1, 9 },
{ 5, 4, 8 }};
int row=3,col=3;
Node head=constructLinkedMatrix(arr,row,col);
display(head);
}
}
class node:
def __init__(self, data):
self.data = data
self.right = None
self.down = None
def newNode(d):
temp = node(d)
return temp
def display(head):
# pointer that will move rightwards
rp = None
# pointer that will move downwards
dp = head
# iterate till down pointer is not None
while (dp != None):
rp = dp
# iterate till right pointer is not None
while rp != None:
print(rp.data, end = ' ')
rp = rp.right
print()
dp = dp.down
def constructLinkedMatrix(mat, m, n):
# array to store starting address of each each row
mainhead = None
head = [0 for i in range(m)]
righttemp = None
newptr = None
# create ‘m’ linked lists for each row
for i in range(m):
# initialize head[i] with None
head[i] = None
for j in range(n):
# create a new node
newptr = newNode(mat[i][j])
# stores the mat[0][0] node as
# the mainhead of the linked list
if (not mainhead):
mainhead = newptr
if (not head[i]):
head[i] = newptr
else:
righttemp.right = newptr
righttemp = newptr
# For every ith row’s list set corresponding down pointers to (i+1)th list’s node
for i in range(m - 1):
temp1 = head[i]
temp2 = head[i + 1]
while (temp1 and temp2):
temp1.down = temp2
temp1 = temp1.right
temp2 = temp2.right
# return the mainhead pointer of the linked list
return mainhead
if __name__ == '__main__':
row = 3
col = 3
mat= [ [ 2, 6, 3 ],
[ 7, 1, 9 ],
[ 5, 4, 8 ] ]
head = constructLinkedMatrix(mat, row, col)
display(head)
Output
2 6 3
7 1 9
5 4 8Time Complexity of 2D linked list : O(n*m), where n is the number of rows in the matrix and m is the number of columns in the matrix.
Conclusion
This article covered how to construct a 2D linked list in which we will see the linked list matrix, having a good grasp of a linked list can be a huge plus point in a coding interview for a better experience you can visit our linked list questions list which will helpful for you. These questions are curated by our expert mentors at PrepBytes, you can follow this link Linked List.
FAQs related to 2D linked list
1. How do you create a 2D linked list in java?
public static LinkedList <String, Double> ll = new LinkedList <String, Double>; java. List.
2. What is a 2D array in data structure?
A two-dimensional array is a data structure that contains cells in a two-dimensional grid which is similar to a table with rows and columns.
3. What is a 2D matrix?
The 2D array is organized as matrices which can be represented as a collection of rows and columns.