Last Updated on March 23, 2022 by Ria Pathak
Concepts Used :
Heap
Difficulty Level :
Easy
Problem Statement :
Given an array containing N integers, our task is to:
- Create min-heap with 1 based indexing.
- Remove the element present at index k from the heap created in the first step using Decrease key method.
- Print the updated heap after second step.
See original problem statement here
Solution Approach :
Introduction :
Our task is pretty straight forward, we just need to perform two operations :
- Create a min-heap.
- Delete an element at given position
kwith decreaseKey().
Method 1 :
We can use sorting algorithms to sort our array in increasing order, and delete
kthvalue of the array. Now print the remaining array.
Method 2(Using Heap) :
In a min-heap, the root always stores the smaller value as compared to its left & right subtree, this condition needs to be true for every node. We need to insert each item one by one such that it’s parent is always smaller than the item itself. If the parent is greater then we need to swap the current item with its parent.
In the deletion process, we can only delete any item if it is the root. So, first we need to take the item (to be deleted), in the root’s position then extract it (remove) using decreaseKey() and store the last item of the heap in the root and reduce the size of our heap by 1.
Since, now the last item is stored in the root’s place this might void the heap property. So, we need to heapify the last node placed at the position of root.
Below is the algorithm of above approach.
Algorithms :
Insert() :
- Insert the item at the last index, and increment the size by 1.
- Then, check if the inserted item is smaller than its parent,
- If yes, then swap the inserted item with its parent.
- If no, then do nothing.
- Now, go to step
2and repeat untill we reach root (first element).
decreaseKey():
- Take the index of the element to be removed.
- Assign the least possible value in the index position.
- Swap the value at this index untill it takes root’s position.
- extract() it and call heapify() since we just removed a node and this might void the heap property.
Extract() :
- Store the value of the first node of our heap (
temp = heap[0]).- Replace the root node with the farthest right node (last element).
(heap[0] = heap[size-1])- Decrease the size by
1.- Perform heapify starting from the new root.
- Return the stored value (
temp).
Heapify():
- if the heap property holds true then you are done.
- else if
- the replacement node value > then swap them, and repeat step 3.
- else
- swap the replacement node with the smallest child node, and
repeat step 3.
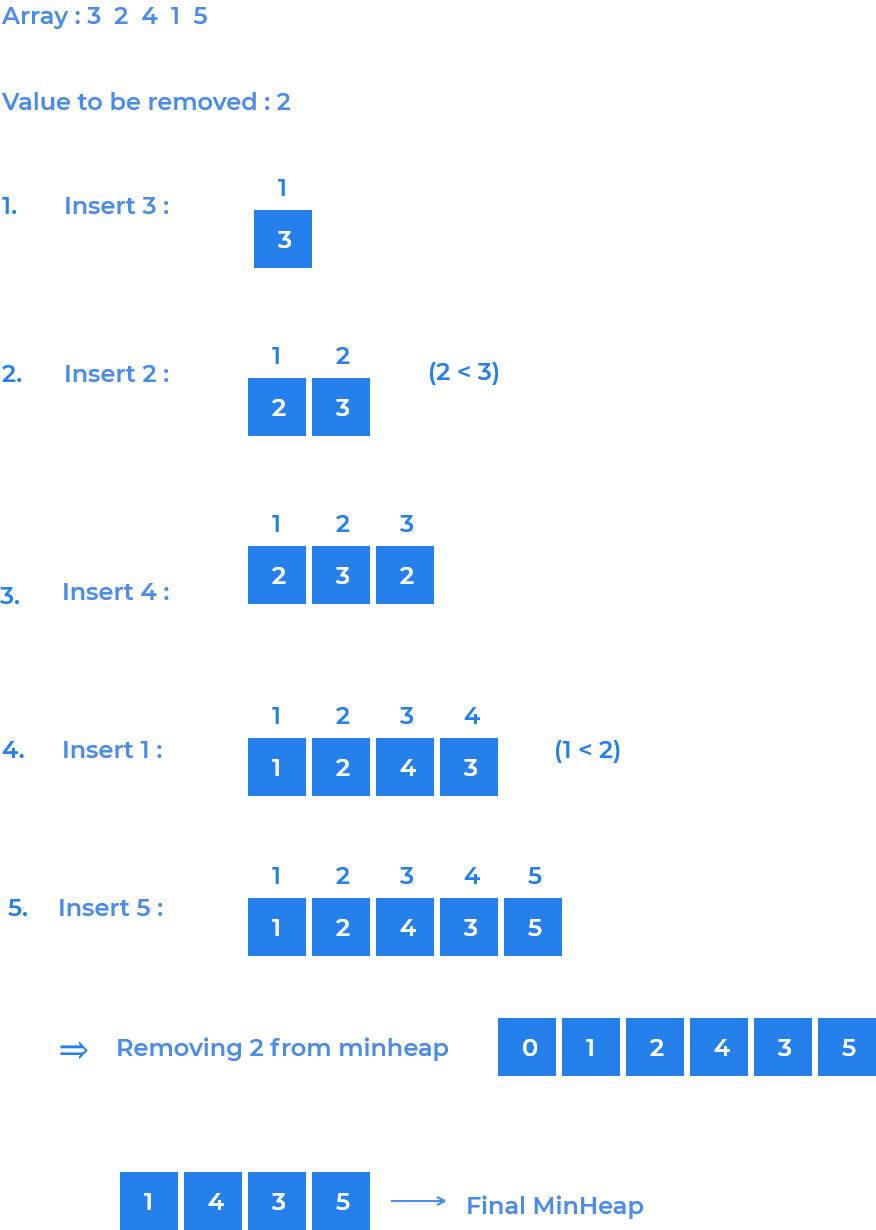
Example:
Solutions:
#include <stdio.h>
#include<stdlib.h>
#define INT_MIN -99999
void swap(int *a,int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
int parent(int i)
{
return (i/2);
}
int left(int i)
{
return (i*2);
}
int right(int i)
{
return (i*2)+1;
}
void insert(int heap[],int *size,int val)
{
int i = (*size);
*size +=1;
heap[i] = val;
while(i!=1 && heap[parent(i)]>heap[i])
{
swap(&heap[parent(i)],&heap[i]);
i = parent(i);
}
//cout<<size;
}
int extract(int heap[],int *size)
{
int root = heap[1];
heap[1] = heap[(*size)-1];
(*size)--;
return root;
}
void heapify(int heap[],int i,int size)
{
int l = left(i);
int r = right(i);
int s = i;
if(l<size && heap[l]< heap[i])
s = l;
if(r<size && heap[r]< heap[s])
s = r;
if(s!=i)
{
swap(&heap[i],&heap[s]);
heapify(heap,s,size);
}
}
void removee(int heap[],int i,int *size)
{
heap[i] = INT_MIN;
while(i!=1 && heap[parent(i)]>heap[i])
{
swap(&heap[parent(i)],&heap[i]);
i = parent(i);
}
extract(heap,size);
heapify(heap,1,*size);
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,k;
int size = 1;
scanf("%d %d", &n,&k);
int *heap =(int*) malloc(sizeof(int)*(n+1));
int a[n];
for(int i = 0;i<n;i++)
{
scanf("%d", &a[i]);
insert(heap,&size,a[i]);
}
removee(heap,k,&size);
for(int j=1;j<size;j++)
printf("%d ", heap[j]);
printf("\n");
}
return 0;
}
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int t=sc.nextInt();
while(t-->0) {
int n = sc.nextInt();
int k = sc.nextInt();
MinHeap minHeap = new MinHeap(n);
for (int i = 0; i < n; i++) {
minHeap.insert(sc.nextInt());
}
minHeap.deleteKey(k);
minHeap.printHeap(sc);
System.out.println();
}
}
}
class MinHeap
{
private int[]Heap;
private int size;
private int maxSize;
private static final int FRONT = 1;
MinHeap(int maxSize)
{
this.maxSize = maxSize;
size=0;
Heap = new int[this.maxSize+1];
Heap[0] = Integer.MIN_VALUE;
}
private int parent(int pos) {
return pos / 2;
}
private int leftChild(int pos)
{
return (2*pos);
}
private int rightChild(int pos)
{
return (2*pos)+1;
}
private boolean isLeaf(int pos)
{
if(pos>=(size/2) && pos<=size)
return true;
return false;
}
private void swap(int fpos, int spos)
{
int temp;
temp = Heap[fpos];
Heap[fpos]=Heap[spos];
Heap[spos]=temp;
}
private void minHeapify(int pos)
{
int left = leftChild(pos);
int right = rightChild(pos);
int largest = pos;
if(left<=size && Heap[left]<Heap[largest])
largest=left;
if(right<=size && Heap[right]<Heap[largest])
largest = right;
if(largest!=pos)
{
swap(pos, largest);
minHeapify(largest);
}
}
void insert(int element)
{
if(size>=maxSize)
return;
Heap[++size]=element;
int i=size;
while(Heap[i]<Heap[parent(i)])
{
swap(i,parent(i));
i=parent(i);
}
}
private void build_heap()
{
int j=(int)Math.floor(size/2.0);
for(int i=j;i>=1;i--){
minHeapify(i);
}
}
public void heapSort(Writer wr) throws IOException {
build_heap();
int length=size;
for(int i=size;i>=2;i--)
{
swap(1,i);
size--;
minHeapify(1);
}
size=length;
// printHeap(wr);
}
public int remove()
{
int popped = Heap[FRONT];
Heap[FRONT] = Heap[size];
size=size-1;
minHeapify(FRONT);
return popped;
}
public void deleteKey(int i)
{
decreaseKey(i, Integer.MIN_VALUE);
remove();
}
private void decreaseKey(int i, int new_val) {
Heap[i]=new_val;
while(i !=0 && Heap[parent(i)]>Heap[i])
{
swap(i,parent(i));
i=parent(i);
}
}
void printHeap(Scanner sc) throws IOException {
for(int i=1;i<=size;i++)
{
//wr.write(Heap[i]+" ");
System.out.print(Heap[i]+" ");
}
}
}
[forminator_quiz id="1482"]
This article tried to discuss the concept of Heap. Hope this blog helps you understand and solve the problem. To practice more problems on Heap you can check out MYCODE | Competitive Programming.