Get free ebooK with 50 must do coding Question for Product Based Companies solved
Fill the details & get ebook over email
Thank You!
We have sent the Ebook on 50 Must Do Coding Questions for Product Based Companies Solved over your email. All the best!
Recursion Interview Programming

Generate all Pairs of 0 and 1

Prepbytes

CONCEPTS USED:

Recursion

DIFFICULTY LEVEL:

Hard

PROBLEM STATEMENT(SIMPLIFIED):

Given N pairs of Binary Numbers 0 and 1, your task is to generate all possible combinations such that for each 0 there should be a corresponding 1 in the combination not vice versa. In simple words for every 0 on the left there should be a 1 on the right.

"0011" is a valid combination as for both zeros there are two 1's present in the right.

"0110" is not a valid combination as there is a 1 for the first 0 but no 1 is present for the last 0 on its right.

For Example :

N = 1

Output : 1

Explanation :

All possible combination of pair 1 = "01", but "10" is not a valid pair as there is no valid 1 for 0 on the right of it.
N = 2

Output : 2

Explanation :

All possible combination of pair 2 = "0011", "0101" 
Notice here that for every 0 on the left there is a 1 on the right.

OBSERVATION:

  1. The problem becomes simple to understand if consider 0 as left bracket "(" and 1 as right bracket ")".

  2. Now we just need to balance these brackets in all possible ways.

  3. For N = 3, such possible combinations can be:
    ((())),
    (()()),
    (())(),
    ()(()),
    ()()()

Can we use Recursion here ?

Yes, Recursion seem to be a great option whenever we need to find different combinations.

SOLVING APPROACH:

  1. We will follow a recursive approach to solve the problem.

  2. Initialize an empty string Str = "" for keeping our resultant string.

  3. Initialize Zeros, Ones for number of zeros and ones, both set to 0 initially.

  4. Keep i = 0 for tracking on which index we are currently on, whenever we reach i = N, this implies we have processed the entire string of length N, just print the Str and return.

  5. On each recursive call, check if Zeros > Ones and Zeros is less than half of N, this implies that Zeros is more in number in the current string and also some 0‘s still remain for getting into the string, in this case, we can either add 0 or 1 to the current string Str, increment i by 1 and increment Zeros/Ones by 1 whoever added.

  6. Else if Zeros is equal to Ones, we can only add 0 to Str, increment i and Zeros by 1.

  7. Else(when all zeros are used / zeroes are in majority), we can add 1 to Str and increment Ones and i by 1.

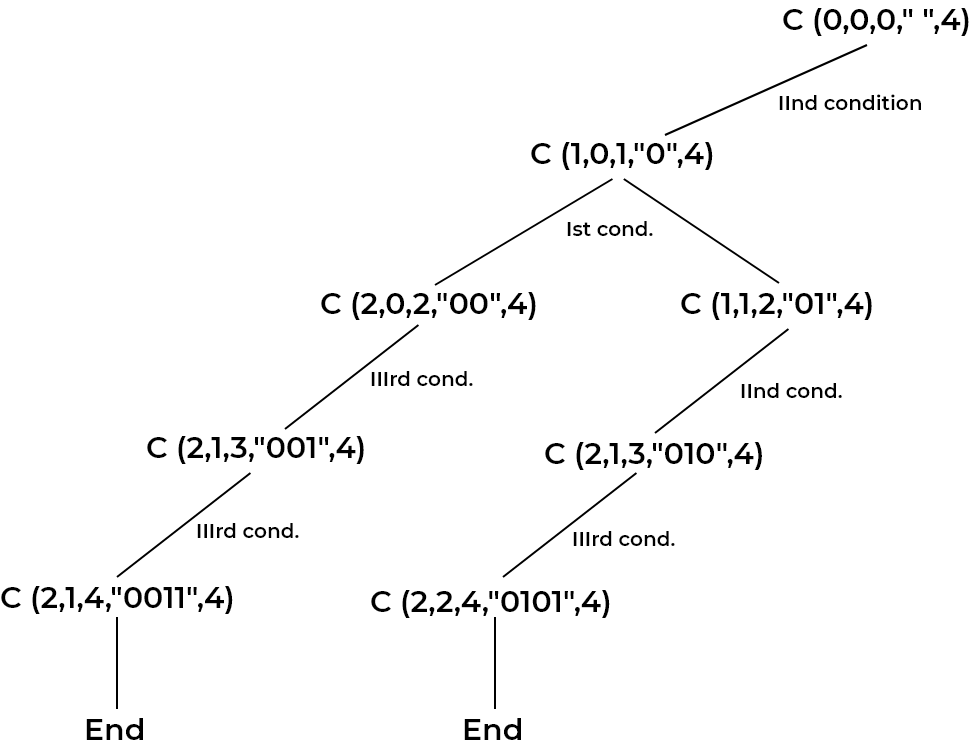
STATE SPACE TREE:


SOLUTIONS:

#include <stdio.h>
#include <string.h>

/* function for appending a char to a char array */
void append(char* s, char c) {
        int len = strlen(s);
        s[len] = c;
        s[len+1] = '\0';
}

//function generating all such combinations
void generatePairs_0_1(int n, int zeros, int ones, char *ans, int i){

  // when i becomes equal to string length print the string
  if(i == n){
    printf("%s ", ans);
    return ;
  }

  /* creating temporary char arrays */
    char temp_0[30];
    char temp_1[30];

    /* copying original char array to temp arrays */
    strcpy(temp_0, ans);
    strcpy(temp_1, ans);

    /* append char i to char array str */
    append(temp_0, '0');
    append(temp_1, '1');

  /*when zeros are greater than ones in the left and half of the
  zeros are not filled  we can either add 0 or 1 to the string */
  if((zeros > ones) && (zeros < n/2)){

    generatePairs_0_1(n, zeros + 1, ones, temp_0, i+1);
    generatePairs_0_1(n, zeros, ones + 1, temp_1, i+1);
  }

  /*when zeros are equal to ones, we can only add 0 zero to the string */
  else if(zeros == ones){
    generatePairs_0_1(n, zeros + 1, ones, temp_0, i+1);
  }

  /*when zeros are greater than ones but have already been
    filled in half of the string, we can now add remaining 1's*/
  else
    generatePairs_0_1(n, zeros, ones + 1, temp_1, i+1);
}

int main()
{
  int n; scanf("%d", &n);

  char ans[30] = "";
  generatePairs_0_1(n*2, 0, 0, ans, 0);

  return 0;
}

#include <bits/stdc++.h>
using namespace std;

//function generating all such combinations
void generatePairs_0_1(int n, int zeros, int ones, string str, int i){

  // when i becomes equal to string length print the string
  if(i == n){
    cout<<str<<" ";
    return ;
  }

  /*when zeros are greater than ones in the left and half of the
  zeros are not filled  we can either add 0 or 1 to the string */
  if((zeros > ones) && (zeros < n/2)){
    generatePairs_0_1(n, zeros + 1, ones, str + "0", i+1);
    generatePairs_0_1(n, zeros, ones + 1, str + "1", i+1);
  }

  /*when zeros are equal to ones, we can only add 0 zero to the string */
  else if(zeros == ones){
    generatePairs_0_1(n, zeros + 1, ones, str + "0", i+1);
  }

  /*when zeros are greater than ones but have already been
    filled in half of the string, we can now add remaining 1's*/
  else
    generatePairs_0_1(n, zeros, ones + 1, str + "1", i+1);
}

int main()
{
  int n; cin>>n;
  generatePairs_0_1(n*2, 0, 0, "", 0);

  return 0;
}

import java.util.*;
import java.io.*;

public class Main {
  static void generatePairs_0_1(int n, int zeros, int ones, String str, int i){

    // when i becomes equal to string length print the string
    if(i == n){
      System.out.print(str + " ");
      return ;
    }

    /*when zeros are greater than ones in the left and half of the
    zeros are not filled  we can either add 0 or 1 to the string */
    if((zeros > ones) && (zeros < n/2)){
      generatePairs_0_1(n, zeros + 1, ones, str + "0", i+1);
      generatePairs_0_1(n, zeros, ones + 1, str + "1", i+1);
    }

    /*when zeros are equal to ones, we can only add 0 zero to the string */
    else if(zeros == ones){
      generatePairs_0_1(n, zeros + 1, ones, str + "0", i+1);
    }

    /*when zeros are greater than ones but have already been
      filled in half of the string, we can now add remaining 1's*/
    else
      generatePairs_0_1(n, zeros, ones + 1, str + "1", i+1);
  }

  public static void main(String args[]) throws IOException {

    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    String res = "";
    generatePairs_0_1(n*2, 0, 0, res, 0);
  }
}

def generatePairs_0_1(n, zeros, ones, str, i):

	if(i == n):
		print(str, end = " ")
		return
	
	if((zeros > ones) and (zeros < n//2)):
		generatePairs_0_1(n, zeros + 1, ones, str + "0", i+1)
		generatePairs_0_1(n, zeros, ones + 1, str + "1", i+1)
	
	elif(zeros == ones):
		generatePairs_0_1(n, zeros + 1, ones, str + "0", i+1)
	
	else:
		generatePairs_0_1(n, zeros, ones + 1, str + "1", i+1)

n = int(input())
generatePairs_0_1(n*2, 0, 0, "", 0)

[forminator_quiz id="1134"]

Space Complexity: O(N)

The space complexity can be reduced to O(N) if Global variable or Static variable is used to store the output string.

Refer Video for Quick Explaination:

Myself

This article tried to discuss Recursion. Hope this blog helps you understand and solve the problem. To practice more problems on Recursion you can check out .

Leave a Reply

Close

Related Post