Grey Code

Last Updated on March 28, 2022 by Ria Pathak

Concepts Used

Back Tracking

Difficulty Level

Hard

Problem Statement :

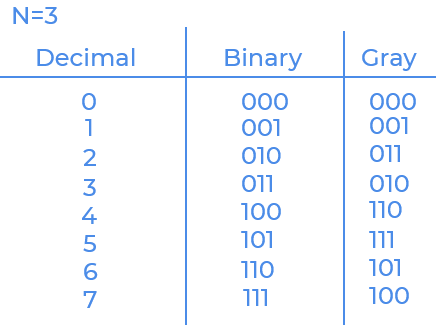
Given a non-negative integer n representing the total number of bits , we need to print the sequence of gray code. In gray code each consecutive code(binary) differs by only one bit.

See original problem statement here

Solution Approach :

Introduction :

Idea is to traverse for every bit and for each bit we can either keep it the way it is or flip it (0->1 or 1->0).

Description:

We will use backtracking to solve the above problem.
Backtracking is the approach to solve the problem by testing all possible answers (by breaking the problems into subproblems). If any subproblem does not fit the given constraint then we discard the complete subproblem (backtrack), moves a step back then try other remaining possible combinations. Backtracking algorithm is generally exponential in time.
For each bit in the number we have two choices, we can either leave it as it is or toggle it, that way our overall bits has atmost difference of 1. We will store the generated value(bits) in a different variable,lets say, ans, so for each recursive call the value of ans would be,

• ans= previous value
• ans = new value(inverted bits)

Suppose if our numer is 3, binary representation of 3 is 0011. Now if we fix the last bit and toggle the second last bit 0001 the difference is of 1 bit between the actual and the new number.
We will keep performing above operations each time by decrementing the value, if the value becomes 0, we print the generated number .

Algorithm :

gray():

1. If number == 0, print ans.
2. else, :
   • recursively call, gray(number-1,ans).
   • toggle the bits in ans, ans = flipBits(ans).
   • recursively call the function with updated ans, gray(number-1,ans).

Complexity Analysis :

In this method each bit has 2 different choices (either leave the bits unchanged or flip the bits) and we have n bits. So the total time complexity is n2ⁿ , where n is the number of bits.

Solutions:

#include <stdio.h>
    #include <math.h>


    int* grayCode(int n, int* returnSize){
        int *out = NULL;

        *returnSize = 0;

        if(n >= 0)
        {
            *returnSize = pow(2, n);
            out = (int *)malloc(sizeof(int)*(*returnSize));

            if(out)
            {
                out[0] = 0;

                if(n >= 1)
                {
                    int i = 0, prev_total = 2;
                    out[1] = 1;

                    for(i=1;i<n;i++)
                    {
                        int j;
                        for(j=0;j<prev_total;j++)
                        {
                            out[prev_total*2-1-j] = out[j] | (1 << i);
                        }
                        prev_total *= 2;
                    }   
                }
            }
        }

        return out;
    }

    int main()
    {
      int n;
      int size = pow(2,n);
      scanf("%d",&n);
      int *out = (int *)malloc(sizeof(int)*(size));
      out = grayCode(n,&size);
      for(int i=0;i<size;i++)
       printf("%d\n",out[i]);

      return 0;
    }

#include <iostream> 
    #include <vector> 
    using namespace std; 

    void gray(int n, int &num) 
    { 
      if(n==0)
      {
            cout<<num<<endl;
            return; 
        } 

        // ignore the bit. 
        gray( n - 1, num); 

        num = num ^ (1 << (n - 1));  //reverse the bit

        gray(n - 1, num); 
    } 



    int main() 
    { 
        int n ;
        cin>>n;
        int k=0;
        gray(n,k);
        return 0; 
    } 

import java.util.*; 

    class Main
    { 

    static int num; 

    static void grayCodeUtil(Vector<Integer> res, int n) 
    { 

        if (n == 0) 
        { 
            res.add(num); 
            return; 
        } 

        // ignore the bit. 
        grayCodeUtil(res, n - 1); 

        // invert the bit. 
        num = num ^ (1 << (n - 1)); 
        grayCodeUtil(res, n - 1); 
    } 

    static Vector<Integer> grayCodes(int n) 
    { 
        Vector<Integer> res = new Vector<Integer>(); 

        num = 0; 
        grayCodeUtil(res, n); 

        return res; 
    } 


    public static void main(String[] args) 
    { 
    Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        Vector<Integer> code = grayCodes(n); 
        for (int i = 0; i < code.size(); i++) 
            System.out.println(code.get(i)); 
    } 
    } 

[forminator_quiz id="1975"]

This article tried to discuss Backtracking. Hope this blog helps you understand and solve the problem. To practice more problems on backtracking you can check out MYCODE | Competitive Programming.