Creating Words

Last Updated on March 28, 2022 by Ria Pathak

Concepts Used

Back Tracking

Difficulty Level

Hard

Problem Statement :

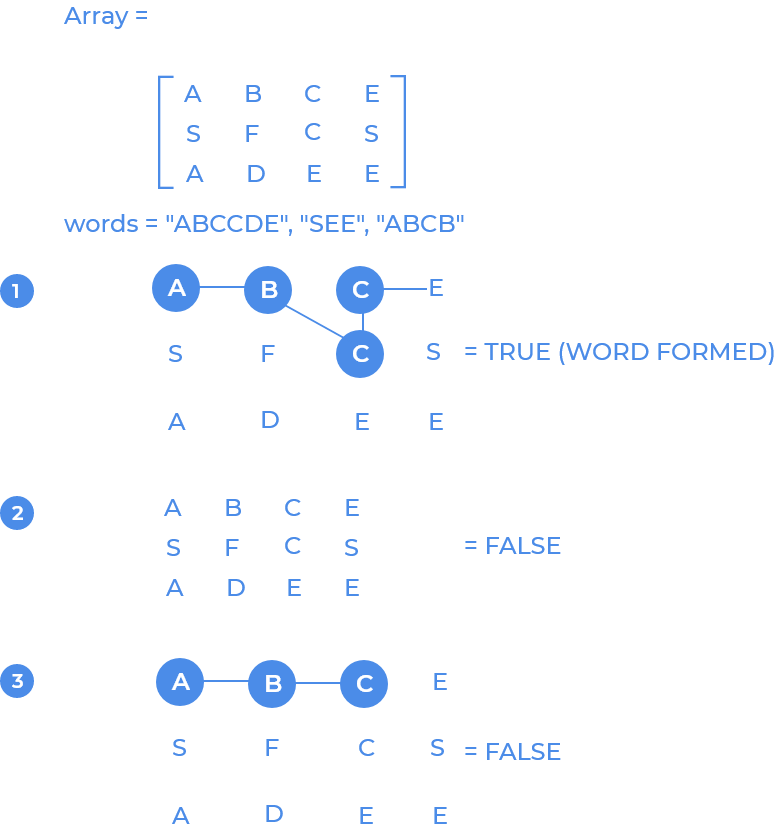
Given a matrix of characters with n rows and m columns, and few words. We have to find out if the words can be formed by a series of adjacent elements. Print "Yes" if words can be formed with adjacent elements else print "No".

See original problem statement here

Solution Approach :

Introduction :

Idea is to iterate for every character in the matrix and check if there is any adjacent character which matches with the character of word, if it does keep check for next character of the word untill the complete word is formed with adjacent characters in matrix.

Description:

We will use backtracking to solve the above problem.
Backtracking is the approach to solve the problem by testing all possible answers (by breaking the problems into subproblems). If any subproblem does not fit the given constraint then we discard the complete subproblem (backtrack), moves a step back then try other remaining possible combinations. Backtracking algorithm is generally exponential in time.
As discussed above we will iterate through each character of the matrix and see if any of the character matches with the character of the word. If it matches then we will recursively check for the next character in the word if it matches. We will return true if all the character in the words matches, else return false. We also have to keep track of the checked characters so that any character must not be checked twice. If some of the subproblems (recursive calls) fails, we will mark the characters as unvisited again so we can again use them for checking.

Algorithm :
bk():

1. if index==wordsize, return TRUE.
2. if i<0 or j=n or j>=m, return FALSE.
3. store the current character, temp = a[i][j].
4. change the current character to mark it visited or used.
5. recurvisely call bk() for all four adjacent cells, if any of the calls return true, assign the original character to a (a[i][j]= temp) & return TRUE..
6. if none of the previous calls has returned true, return FALSE

Complexity Analysis :

We are making four recursive calls each time and for every new call again 4 recursive calls . So the time complexity would grow exponentially! Can you guess the time complexity?

Solutions:

#include <bits/stdc++.h>
    using namespace std;

    int bk(vector<vector<char>> &a,const int i,const int j,const int k,const string &b,const int n,const int m,const int size)
    {

       if(k>=size)
      {
        return 1;
      }

      if(i>=n || j>=m ||k>=size|| i<0 || j<0)
      {
        return 0;
      }

          char ch = a[i][j];
          if(ch!=b[k]|| a[i][j]=='#')
           return 0;

          a[i][j] = '#';
          if( bk(a,i-1,j,k+1,b,n,m,size)==1 
              || bk(a,i+1,j,k+1,b,n,m,size)==1
              ||bk(a,i,j-1,k+1,b,n,m,size)==1 
              || bk(a,i,j+1,k+1,b,n,m,size)==1 )
          {
            a[i][j]=ch;
            return 1;
          }
          a[i][j] = ch;


      return 0;
    }

    int main()
    {
      int n,m;
      cin>>n>>m;
      vector<vector<char>> a(n);

      for(int i=0;i<n;i++)
      {
        for(int j=0;j<m;j++)
        {
          char t;
          cin>>t;
          a[i].push_back(t);
        }
      }

      int q;
      cin>>q;
      while(q--)
      {
        string str;
        cin>>str;
        int size = str.length();
        int flag = 0;
        for(int i=0;i<n;i++)
        {
          for(int j=0;j<m;j++)
          {
            int k=0;
            if(bk(a,i,j,k,str,n,m,size))
              flag = 1;
          }
        }

        (flag)?cout<<"Yes"<<endl: cout<<"No"<<endl;
      }

      return 0;
    }

import java.util.*;
  import java.io.*;

  public class Main {
    static boolean visited[][];
    public static void main(String args[]) throws IOException {

      Scanner sc=new Scanner(System.in);
      int rows=sc.nextInt();
      int column=sc.nextInt();
      char array[][]=new char[rows][column];

      for(int i=0;i<rows;i=i+1)
      {
        for(int j=0;j<column;j=j+1)
        {
          array[i][j]=sc.next().charAt(0);
        }
      }

      int t=sc.nextInt();
      for(int i=0;i<t;i=i+1)
      {
        visited=new boolean[rows][column]; 
        boolean answer=recursion(rows,column,array,sc.next());
        if(answer==true)
          System.out.println("Yes");
        else
          System.out.println("No");
      }
    }

    static boolean recursion(int rows,int column,char array[][],String word)
    {
      for(int i=0;i<rows;i=i+1)
      {
        for(int j=0;j<column;j=j+1)
        {
          if(word.charAt(0)==array[i][j]  &&  searchWord(rows,column,i,j,array,word,0))
          {
            return true;
          }
        }
      }
      return false;
    }

    static boolean searchWord(int rows,int column,int i,int j,char array[][],String word,int index)
    {
      if(index==word.length())
        return true;

      if(i<0 || i>=rows || j<0 || j>=column || word.charAt(index)!=array[i][j] || visited[i][j])
      {
        return false;
      }

      visited[i][j]=true;

      if(searchWord(rows,column,i+1,j,array,word,index+1) ||
      searchWord(rows,column,i-1,j,array,word,index+1) ||
      searchWord(rows,column,i,j+1,array,word,index+1) ||
      searchWord(rows,column,i,j-1,array,word,index+1))
      {
        return true;
      }

      visited[i][j]=false;
      return false;
    }
  }

[forminator_quiz id="2015"]

So, in this blog, we have tried to explain backtracking. If you want to solve more questions on backtracking, which are curated by our expert mentors at PrepBytes, you can follow this link Backtracking.