Get free ebooK with 50 must do coding Question for Product Based Companies solved
Fill the details & get ebook over email
Thank You!
We have sent the Ebook on 50 Must Do Coding Questions for Product Based Companies Solved over your email. All the best!
Linked list articles

Types of Linked list

Abhinav Trivedi

Last Updated on April 22, 2023 by Prepbytes

Linked list is a linear data structure consisting of nodes, where each node contains a value and a reference to the next (and possibly previous) node. This structure allows for dynamic memory allocation and easy insertion and deletion of elements. There are various types of linked lists which differ in their structure and functionality. This article discusses all types of linked lists, as well as the applications and representation of each linked list.

Types of Linked Lists

Each variant of linked list possesses its own unique characteristics and varies from other linked lists in terms of how it is constructed and how it operates. The section below provides a comprehensive explanation of all types of linked lists.

1. Singly Linked List

Here’s a simplified explanation of a singly linked list:

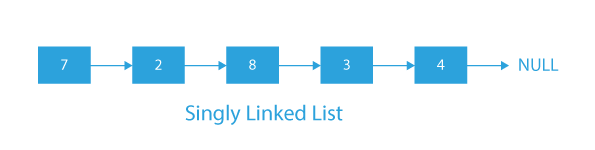
  • A singly linked list is a basic type of data structure that consists of a series of nodes.
  • Each node in the singly linked list has two components: a data value and a pointer to the next node.
  • The first node in the singly linked list is called the head, and the last node is called the tail. The tail’s pointer points to null, indicating the end of the list.
  • A singly linked list is traversed only in one direction, from the head to the tail, as only unidirectional traversal is possible.
  • Singly linked lists are often used in computer programming to implement other data structures, such as stacks and queues, and to represent relationships between objects.

The image below clearly depicts the appearance of the singly linked list.

Structure of Singly Linked List Node
The code below defines a structure for a singly linked list node.

struct Node {
    int data;
    struct Node* next;
};

class Node {
public:
int data;
// Pointer to next node in LL
Node* next;
};

class Node 
{
    public
        int data;
        Node next;
}

class Node:
    def __init__(self, data=None, next=None):
        self.data = data
        self.next = next

Creation and Traversal of Singly Linked List
Below is the program that demonstrates the creation and traversal of a singly linked list.

#include<stdio.h>
#include<stdlib.h>
// Structure of Node
struct Node {
    int data;
    struct Node* next;
};
 
// This function will print data present in the linked list from 
// start to end
void printList(struct Node* n)
{
 
    // move till n is NULL
    while (n != NULL) {
 
        // Print the data
        printf("%d ",n->data);
        n = n->next;
    }
}
 
// Driver Code
int main()
{
    struct Node* head = NULL;
    struct Node* second = NULL;
   struct Node* third = NULL;
 
    // create 3 nodes with data 
    head = new_Node(10);
    second = new_Node(12);
    third = new_Node(37);
 
    // create a linke from first node to second node
    head->next = second;
 
    // create a linke from second node to third node
    second->next = third;
 
    // make last node’s next as NULL
    third->next = NULL;
 
    printList(head);
 
    return 0;
}

#include <bits stdc++.h="">
using namespace std;
 
// Structure of Node
class Node {
public:
    int data;
    Node* next;
    Node(int x){
    data = x;
    next = NULL;
}
};
 
// This function will print data present in the linked list from 
// start to end
void printList(Node* n)
{
 
    // move till n is NULL
    while (n != NULL) {
 
        // Print the data
        cout << n->data << " ";
        n = n->next;
    }
}
 
// Driver Code
int main()
{
    Node* head = NULL;
    Node* second = NULL;
    Node* third = NULL;
 
    // create 3 nodes with data 
    head = new Node(10);
    second = new Node(12);
    third = new Node(37);
 
    // create a linke from first node to second node
    head->next = second;
 
    // create a linke from second node to third node
    second->next = third;
 
    // make last node’s next as NULL
    third->next = NULL;
 
    printList(head);
 
    return 0;
}

class SinglyLinkedList 
{
    public
        int data;
        SinglyLinkedList next;
        SinglyLinkedList(int data)
        {
            this.data=data;
        }
        static void printList(SinglyLinkedList n)
        {
            while(n!=null)
            {
                System.out.print(n.data+" ");
                n=n.next;
            }
        }
        public static void main(String[] args) 
        {
            SinglyLinkedList head=null;
            SinglyLinkedList second=null;
            SinglyLinkedList third=null;
        
            head =new SinglyLinkedList(10);
            second=new SinglyLinkedList(12);
            third=new SinglyLinkedList(37);

            head.next=second;
            second.next=third;
            third.next=null;

            printList(head);
        }    
}


class Node:
    def __init__(self, data=None, next=None):
        self.data = data
        self.next = next

# This function will print data present in the linked list from start to end
def printList(head):
 
    while (head != None):
        print( head.data , end=" ")
        head = head.next

head = None
second = None
third = None

# create 3 nodes with data 
head = Node(10)
second = Node(12)
third = Node(37)

# create a link from first node to second node
head.next = second

# create a link from second node to third node
second.next = third

printList(head)

Output

10 12 37

Complexity Analysis of Creation and Traversal of Singly Linked List
Here’s the time and space complexity analysis of the above program:

Time Complexity:

  • The creation of each node takes constant time O(1).
  • The linking of the nodes takes constant time O(1).
  • The traversal of the linked list using the "printList" function takes linear time O(n), where n is the number of nodes in the linked list.

Therefore, the overall time complexity of this program is O(n).

Space Complexity:

  • The space complexity of this program depends on the number of nodes in the linked list.
  • Each node requires a constant amount of space for its "data" and "next" members.
  • The head, second, and third pointers require constant space.

Therefore, the overall space complexity of this program is O(n), where n is the number of nodes in the linked list.

2. Doubly Linked List

Here’s a simplified explanation of a doubly linked list:

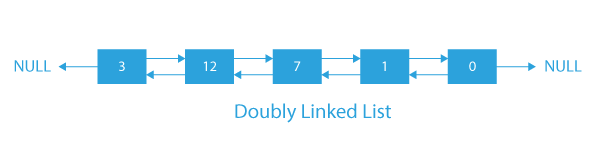
  • Doubly linked list is similar to singly linked list, but has an additional pointer that points to the previous node.
  • Each node in the doubly linked list has three parts: data of the node, a pointer to the next node which has the address of the next node, and another pointer to the previous node which has the address of the previous node.
  • The first node in the doubly linked list is known as the head node, while the last node is called the tail node. The first node’s previous pointer points to the null value, and the last node’s next pointer points to the null value.
  • Doubly linked list is a bi-directional linked list, which means you can traverse it either from head to tail or from tail to head. Here, the pointer to the next node is generally referred to as "next" and the information to the previous node is called "prev".

The image below provides a clear illustration of how doubly linked lists are represented.

Structure of Doubly Linked List Node
The code below defines a structure for a doubly linked list node.

struct node   
{  
    struct node *prev;   
    int data;  
    struct node *next;   
}   

class Node {
public:
int data;
// Pointer to next node in LL
Node* next,*prev;
Node(int x){
    data = x;
    next = NULL;
    prev = NULL;
    }
};

class Node {
public:
int data;
// Pointer to next node in LL
Node* next,*prev;
Node(int x){
    data = x;
    next = NULL;
    prev = NULL;
    }
};

class Node:
    def __init__(self, data=None, next=None, prev=None):
        self.data = data
        self.next = next
        self.prev = prev

Creation and Traversal of Doubly Linked List
Below is the program that demonstrates the creation and traversal of a doubly linked list.

#include <stdio.h>
#include<stdlib.h>

struct node   
{  
    struct node *prev;   
    int data;  
    struct node *next;   
} 
void push(Node** head_ref, int new_data)
{
    // create a new node with given data 
     struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
 
    
 
    // assign head node’s address to next of new node
    new_node->next = (*head_ref);
 
    // assign NULL to prev of new node
    new_node->prev = NULL;
 
    // update the previous of old node as new node
    if ((*head_ref) != NULL)
        (*head_ref)->prev = new_node;
 
    // update the head node of list as new node 
    (*head_ref) = new_node;
}
 
// This function will print data present in the linked list from 
// start to end and also in reverse order
void printList(struct Node* node)
{
    struct Node* last;
 
    printf("\nTraversal in forward direction \n";
    while (node != NULL) {
 
        // Print the data
        pritnf("%d ,node->data);;
        last = node;
        node = node->next;
    }
 
    printf("\nTraversal in reverse direction \n";
    while (last != NULL) {
 
        // Print the data
        printf("%d ,last->data);
        last = last->prev;
    }
}
 
// Driver Code
int main()
{
    // Start with the empty list
    struct Node* head = NULL;
 
    // Insert 10.
    // So linked list becomes 10->NULL
    push(&head, 10);
 
    // Insert 44 at the beginning. So
    // linked list becomes 44->10->NULL
    push(&head, 44);
 
    // Insert 11 at the beginning. So
    // linked list becomes 11->44->10->NULL
    push(&head, 11);
 
    printf("Created DLL is: ");
    printList(head);
 
    return 0;
}

#include <bits stdc++.h="">
using namespace std;
 
// Doubly linked list node
class Node {
public:
    int data;
    Node* next;
    Node* prev;
    Node(int x){
        data = x;
        prev = NULL;
        next = NULL;
    }
};
 
// This function will add a new node in front of the list
void push(Node** head_ref, int new_data)
{
    // create a new node with given data 
    Node* new_node = new Node(new_data);
 
    
 
    // assign head node’s address to next of new node
    new_node->next = (*head_ref);
 
    // assign NULL to prev of new node
    new_node->prev = NULL;
 
    // update the previous of old node as new node
    if ((*head_ref) != NULL)
        (*head_ref)->prev = new_node;
 
    // update the head node of list as new node 
    (*head_ref) = new_node;
}
 
// This function will print data present in the linked list from 
// start to end and also in reverse order
void printList(Node* node)
{
    Node* last;
 
    cout << "\nTraversal in forward"
        << " direction \n";
    while (node != NULL) {
 
        // Print the data
        cout << " " << node->data << " ";
        last = node;
        node = node->next;
    }
 
    cout << "\nTraversal in reverse"
        << " direction \n";
    while (last != NULL) {
 
        // Print the data
        cout << " " << last->data << " ";
        last = last->prev;
    }
}
 
// Driver Code
int main()
{
    // Start with the empty list
    Node* head = NULL;
 
    // Insert 10.
    // So linked list becomes 10->NULL
    push(&head, 10);
 
    // Insert 44 at the beginning. So
    // linked list becomes 44->10->NULL
    push(&head, 44);
 
    // Insert 11 at the beginning. So
    // linked list becomes 11->44->10->NULL
    push(&head, 11);
 
    cout << "Created DLL is: ";
    printList(head);
 
    return 0;
}

class Node:
    def __init__(self, data=None, next=None, prev=None):
        self.data = data
        self.next = next
        self.prev = prev

# This function will add a new node in front of the list
def push(head, new_data):
 
        # create a new node with given data 
        new_node = Node(new_data)
 
        # assign head node’s address to next of new node
        new_node.next = head
 
        # update the previous of old node as new node
        if head is not None:
            head.prev = new_node
 
        # update the head node of list as new node 
        head = new_node
        return new_node
 

# This function will print data present in the linked list from start to end
def printList(node):
 
        print("Traversal in forward direction")
        while node:
            print(node.data,end=" ")
            last = node
            node = node.next
 
        print("\nTraversal in reverse direction",)
        while last:
            print(last.data,end=" ")
            last = last.prev

# Start with the empty list
head = None

# Insert 10.
# So linked list becomes 10->NULL
head = push(head,10)

# Insert 44 at the beginning. So
# linked list becomes 44->10->NULL
head = push(head,44)

# Insert 11 at the beginning. So
# linked list becomes 11->44->10->NULL
head = push(head,11)

print("Created DLL is:")
printList(head)

Output

Created DLL is:
Traversal in forward direction
11 44 10
Traversal in reverse direction
10 44 11

Complexity Analysis of Creation and Traversal of Doubly Linked List
Here’s the time and space complexity analysis of the above program:

Time Complexity:
The time complexity of the program is O(n), where n is the number of nodes in the doubly linked list. Also, each node insertion operation takes O(1) time.

Space Complexity:
The space complexity of the program is O(n), where n is the number of nodes in the doubly linked list. This is because the program uses dynamic memory allocation to create nodes for the linked list, and each node takes O(1) space.

3. Circular Linked List

Here’s an explanation of circular linked list:

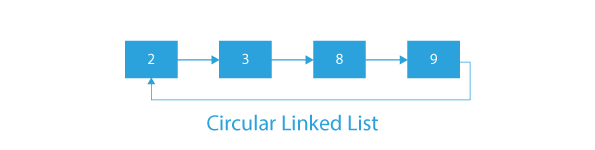
  • A circular linked list is a type of linked list where the last node points to the first node, creating a circular structure.
  • A circular linked list can only be traversed in one direction, making it a unidirectional linked list.
  • Compared to a singly linked list, a circular linked list has no end and can theoretically go on forever, but the traversal must still start at the head node.

The image below provides a clear illustration of how doubly linked lists are represented.

Structure of Circular Linked List Node
The code below defines a structure for a doubly linked list node.

class Node {
public:
int data;
// Pointer to next node in LL
Node* next;
};

Creation and Traversal of Circular Linked List
Below is the program that demonstrates the creation and traversal of circular linked list.

#include <bits stdc++.h="">
using namespace std;
 
// Structure for a node
class Node {
public:
    int data;
    Node* next;
    Node(int x){
    data = x;
    next = NULL;
}
};
 
// This function will insert a node at the beginning of the
// list
void push(Node** head_ref, int data)
{
    Node* ptr1 = new Node(data);
    Node* temp = *head_ref;
    ptr1->next = *head_ref;
 
    if (*head_ref != NULL) {
        while (temp->next != *head_ref) {
            temp = temp->next;
        }
        temp->next = ptr1;
    }
 
    else
        ptr1->next = ptr1;
 
    *head_ref = ptr1;
}
 
// This function will print data of all nodes in the list
void printList(Node* head)
{
    Node* temp = head;
    if (head != NULL) {
        do {
 
            // Print the data
            cout << temp->data << " ";
            temp = temp->next;
        } while (temp != head);
    }
}
 
// Main function
int main()
{
    Node* head = NULL;
    push(&head, 14);
    push(&head, 35);
    push(&head, 5);
    push(&head, 9);
    //created list will be 9->5->35->14
    cout << "Contents of Circular"
        << " Linked List\n ";
    printList(head);
 
    return 0;
}

Output

Contents of Circular Linked List
9 5 35 14

Complexity Analysis of Creation and Traversal of Doubly Linked List
Here’s the time and space complexity analysis of the above program:

Time Complexity:
The time complexity of the push function is O(n) in the worst case, where n is the number of nodes in the circular linked list. This is because in the worst case scenario, the function will need to traverse the entire linked list to find the last node and update its next pointer to point to the newly inserted node.

The time complexity of the printList function is also O(n), where n is the number of nodes in the circular linked list. This is because the function will need to traverse the entire linked list to print the data of each node.

Space Complexity: O(n), where ‘n’ is the number of nodes present in the circular linked list.

4. Doubly Circular Linked List

Here’s an explanation of Doubly Circular Linked List.

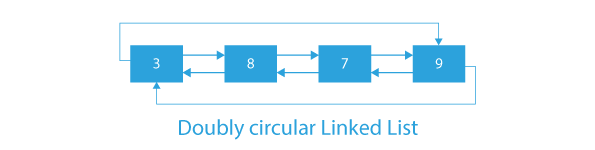
  • A doubly circular linked list is the combination of both a circular linked list and a doubly linked list.
  • Each node in the doubly circular linked list has three parts: one for data, the second for storing the address of the next node, and the last for storing the address of the previous node.
  • A special feature of a doubly circular linked list is that, like a circular linked list, its last node points to the head of the linked list.
  • A doubly circular linked list can be traversed in both directions, making it a bi-directional linked list.

The image below provides a clear illustration of how doubly circular linked lists are represented.

Structure of Doubly Circular Linked List Node
The code below defines a structure for a doubly circular linked list node.

class Node {
public:
int data;
// Pointer to next node in LL
Node* next,*prev;
Node(int x){
    data = x;
    next = NULL;
    prev = NULL;
    }
};

class Node:
	def __init__(self, data=None, next=None, prev=None):
		self.data = data
		self.next = next
		self.prev = prev

Creation and Traversal of Doubly Circular Linked List
Below is the program that demonstrates the creation and traversal of doubly circular linked list.

#include <bits stdc++.h="">
using namespace std;
 
// Structure of a Node
class Node {
public:
int data;
// Pointer to next node in LL
Node* next,*prev;
Node(int x){
    data = x;
    next = NULL;
    prev = NULL;
}
 
};
 
// This function will insert a node at the beginning of the
// list
void insertBegin(Node** start,
                int value)
{
    // when list is empty
    if (*start == NULL) {
        Node* new_node = new Node(value);
        new_node->next
            = new_node->prev = new_node;
        *start = new_node;
        return;
    }
 
    // last node
    Node* last = (*start)->prev;
 
    Node* new_node = new Node(value);
 
    // update the prev and next pointers
    new_node->next = *start;
    new_node->prev = last;
 
    // Update next and previous
    // pointers of start & last
    last->next = (*start)->prev
        = new_node;
 
    // Update start pointer
    *start = new_node;
}
 
// This function will print the data in nodes of our list
void display(Node* start)
{
    Node* temp = start;
 
    printf("\nTraversal in"
        " forward direction \n");
    while (temp->next != start) {
        printf("%d ", temp->data);
        temp = temp->next;
    }
    printf("%d ", temp->data);
 
    printf("\nTraversal in "
        "reverse direction \n");
    Node* last = start->prev;
    temp = last;
 
    while (temp->prev != last) {
 
        // Print the data
        printf("%d ", temp->data);
        temp = temp->prev;
    }
    printf("%d ", temp->data);
}
 
// Driver Code
int main()
{
    // Start with the empty list
     Node* start = NULL;
 
    // Insert 7
    // So linked list becomes 7->NULL
    insertBegin(&start, 7);
 
    // Insert 5 at the beginning
    // So linked list becomes 5->7
    insertBegin(&start, 5);
 
    // Insert 10 at the end
    // So linked list becomes 10->5->7
    insertBegin(&start, 10);
 
    printf("Created circular doubly"
        " linked list is: ");
    display(start);
 
    return 0;
}

Output

Created circular doubly linked list is:
Traversal in forward direction
10 5 7
Traversal in reverse direction
7 5 10

Complexity Analysis of Creation and Traversal of Doubly Circular Linked List
Here’s the time and space complexity analysis of the above program:

Time Complexity:
The time complexity of the insertBegin function is O(1) because it involves only constant-time operations, regardless of the size of the linked list. The display function iterates over all nodes of the linked list. Therefore, its time complexity is O(n), where n is the number of nodes in the linked list.

Space Complexity:
The space complexity of the program is O(n), where n is the number of nodes in the linked list.

Conclusion
In conclusion, linked lists are an essential data structure in computer science that allow for efficient data storage and traversal. The four main types of linked lists include singly linked lists, doubly linked lists, circular linked lists, and doubly circular linked lists. Each type has its own unique features and advantages, and understanding the differences between them is important in choosing the appropriate data structure for a given application. If you want to solve more questions on Linked List, which are curated by our expert mentors at PrepBytes, you can follow this link Linked List.

FAQs related to Linked List

Here are some frequently asked questions on types of linked list.

Q1: What is a singly linked list and how does it differ from other types of linked lists?
Ans: A singly linked list is a type of linked list where each node contains a data element and a pointer to the next node in the list. It differs from other types of linked lists, such as doubly linked lists and circular linked lists, in that it only has one pointer per node.

Q2: What is a doubly linked list and what are its advantages over a singly linked list?
Ans: A doubly linked list is a type of linked list where each node contains a data element and two pointers – one to the next node in the list and one to the previous node. Its advantages over a singly linked list include the ability to traverse the list in both directions and the ability to easily delete nodes from the list.

Q3: What is a circular linked list and what are some use cases for it?
Ans: A circular linked list is a type of linked list where the last node points back to the first node, forming a loop. It is useful in situations where a list needs to be continuously traversed, such as in a queue or circular buffer.

Q4: What is a XOR linked list and what are its advantages over other types of linked lists?
Ans: An XOR linked list is a type of linked list where each node contains a single pointer that is the XOR of the previous and next nodes. Its advantages over other types of linked lists include the ability to save space by using only one pointer per node and the ability to traverse the list in both directions.

Q5: What is a lock-free linked list and how does it differ from other types of linked lists?
Ans: A lock-free linked list is a type of linked list where multiple threads can concurrently access and modify the list without using locks or other synchronization mechanisms. It differs from other types of linked lists in that it is designed to be thread-safe without the use of locks.

Leave a Reply

Your email address will not be published. Required fields are marked *

Close

Related Post