Get free ebooK with 50 must do coding Question for Product Based Companies solved
Fill the details & get ebook over email
Thank You!
We have sent the Ebook on 50 Must Do Coding Questions for Product Based Companies Solved over your email. All the best!
Linked list articles

Merge a Linked List into another Linked List at alternate positions

Aman Sharma

Last Updated on July 31, 2023 by Mayank Dham

In this article, we dive into the solution to merge a linked list into another linked list at alternate positions, exploring different approaches and algorithms that pave the way for seamless integration. We will uncover how this technique not only conserves memory but also facilitates enhanced time complexity, making it an invaluable tool for developers in various programming domains. Linked list is a linear dat a structure of connected nodes, and each node consists of two parts. One part is data, where the value of the node is stored and the other part is next, which is a pointer to the next node. Let’s discuss completely how to merge two linked list alternatively.

How to Merge Two Linked List Alternatively

In this problem, we are given two linked lists, A and B. We should merge the second list into the first one at alternate positions. The second linked list should become empty.

Let’s try to understand this problem with help of examples.

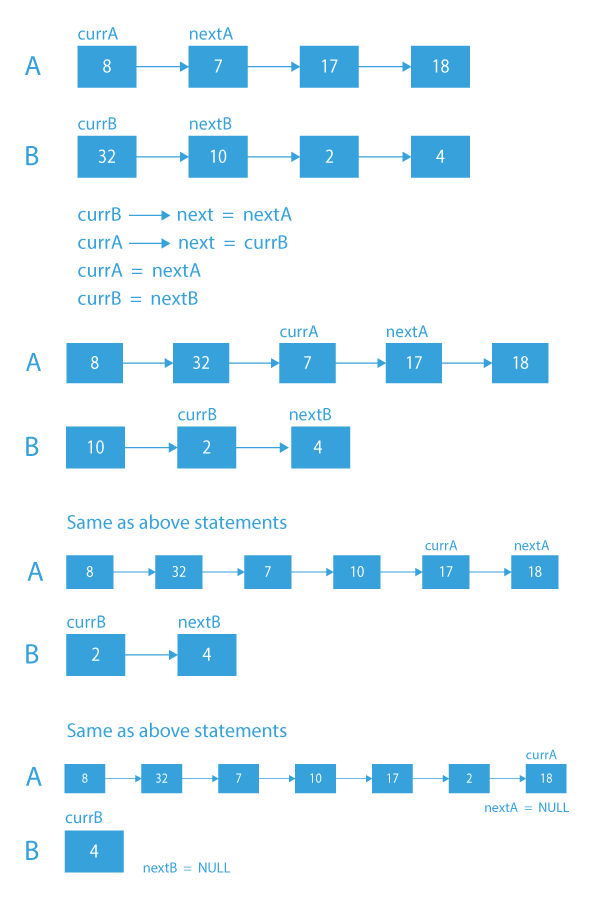
Suppose the given linked lists are:

We have add the elements of the second list to the first list, at alternate positions.

  • First, we will add the first element of B after the first element of A –

  • Now, add the second element of B after the second element of old A –

  • Now, add the third element of B after the third element of old A

  • Now, add the fourth element of B after the fourth element of old A

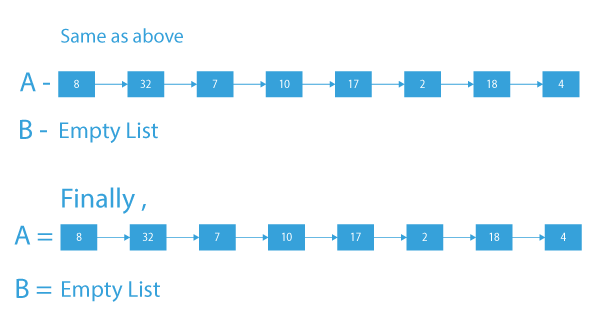
    B: Empty list

After adding the elements of the second list to the first list at alternate positions, the final list will be:

Input:

Output:

Explanation:The nodes of the second linked list are merged with the first linked list at alternate positions.

I think from the above example the problem statement is clear, so we should now think how we can approach this problem. Try to come up with a approach, it may be bruteforce but before jumping to approach section try to think how will you approach it.

Note: We should keep in mind that we cannot create a new linked list. We have to alter the first list.

Approach of merge two linked list alternatively

The main idea is to iterate using a loop while there are available positions in the first list and insert nodes of the linked list by changing pointers. We should also note that the head of the first link will never change, but the head of the second list may change, so we have to use one pointer for the first list and two pointers for the second list. We can get a better idea by looking at the algorithm.

Algorithm of merge two linked list alternatively

  • Traverse in FirstList until there are available positions in it.
  • Loop in SecondList and insert nodes of SecondList to FirstList.
  • Do insertion by changing pointers.
  • Store next pointers of both A and B in nextA and nextB and current pointers of both A and B in currA and currB.
  • Make B as the next of pointer A and next of pointer B is next of pointer A. By doing this we insert a node of SecondList in FirstList:
    currB – > next = nextA
    currA – > next = currB
    currA=nextA
    currB=nextB
  • Move pointers of FirstList and SecondList and again perform the above steps of insertion of list B nodes in list A at alternate position.

Dry Run of merge two linked list alternatively


Code Implementation of merge two linked list alternatively

#include <stdio.h>
#include <stdlib.h>
 
// A nexted list node
struct Node
{
    int data;
    struct Node *next;
};
 
/* Function to insert a node at the beginning */
void push(struct Node ** head_ref, int new_data)
{
    struct Node* new_node =
           (struct Node*) malloc(sizeof(struct Node));
    new_node->data  = new_data;
    new_node->next = (*head_ref);
    (*head_ref)  = new_node;
}
 
/* Utility function to print a singly linked list */
void printList(struct Node *head)
{
    struct Node *temp = head;
    while (temp != NULL)
    {
        printf("%d ", temp->data);
        temp = temp->next;
    }
    printf("\n");
}
 
// Main function that inserts nodes of linked list q into p at
// alternate positions. Since head of first list never changes
// and head of second list  may change, we need single pointer
// for first list and double pointer for second list.
void merge(struct Node *p, struct Node **q)
{
     struct Node *p_curr = p, *q_curr = *q;
     struct Node *p_next, *q_next;
 
     // While there are available positions in p
     while (p_curr != NULL && q_curr != NULL)
     {
         // Save next pointers
         p_next = p_curr->next;
         q_next = q_curr->next;
 
         // Make q_curr as next of p_curr
         q_curr->next = p_next;  // Change next pointer of q_curr
         p_curr->next = q_curr;  // Change next pointer of p_curr
 
         // Update current pointers for next iteration
         p_curr = p_next;
         q_curr = q_next;
    }
 
    *q = q_curr; // Update head pointer of second list
}
 
// Driver program to test above functions
int main()
{
     struct Node *p = NULL, *q = NULL;
     push(&p, 3);
     push(&p, 2);
     push(&p, 1);
     printf("First Linked List:\n");
     printList(p);
 
     push(&q, 8);
     push(&q, 7);
     push(&q, 6);
     push(&q, 5);
     push(&q, 4);
     printf("Second Linked List:\n");
     printList(q);
 
     merge(p, &q);
 
     printf("Modified First Linked List:\n");
     printList(p);
 
     printf("Modified Second Linked List:\n");
     printList(q);
 
     getchar();
     return 0;
}

#include <bits stdc++.h="">
using namespace std;
struct LLNode
{
    int data;
    struct LLNode* next;
};

void insertAtBeginning(struct LLNode** head, int dataToBeInserted)
{
    struct LLNode* curr = new LLNode;
    curr->data = dataToBeInserted;
    curr->next = NULL;    
    if(*head == NULL)
            *head=curr; 
        
    else
        {
            curr->next=*head;
            *head=curr;
        }
        
       
}

void display(struct LLNode**node)
{
    struct LLNode *temp= *node;
    if (temp==NULL)
    {
        cout<<"Empty linked list"<<endl; }="" while(temp!="NULL)" {="" if(temp-="">next!=NULL)
            cout<<temp->data<<" ->";
            else
            cout<<temp->data;
            
            temp=temp->next;
        }
    cout<<endl; }="" void="" merge(struct="" llnode="" *a,="" struct="" **b)="" {="" *curra="A," *currb="*B;" *nexta,="" *nextb;="" while="" (curra="" !="NULL" &&="" currb="" nexta="currA-">next;
         nextB = currB->next;
         currB->next = nextA;  
         currA->next = currB;  
         currA = nextA;
         currB = nextB;
    }
    *B = currB;
}

int main()
{
     struct LLNode *FirstList = NULL, *SecondList = NULL;
     insertAtBeginning(&FirstList, 18);
     insertAtBeginning(&FirstList, 17);
     insertAtBeginning(&FirstList, 7);
     insertAtBeginning(&FirstList, 8);
     
     insertAtBeginning(&SecondList, 4);
     insertAtBeginning(&SecondList, 2);
     insertAtBeginning(&SecondList, 10);
     insertAtBeginning(&SecondList, 32);
     cout<<"Linked List A: ";
     display(&FirstList);
 
     cout<<"Linked List B: ";
     display(&SecondList);
    
     cout<<"Merging List B into List A at alternate positions in A";
     Merge(FirstList,&SecondList);
 
     cout<<"\nOutput Linked List A: ";
     display(&FirstList);
 
     cout<<"Output Linked List B: ";
     display(&SecondList);
 
     return 0;
}


public class LinkedList
{
    Node head; 
 

    class Node
    {
        int data;
        Node next;
        Node(int d) {data = d; next = null; }
    }

    void push(int new_data)
    {

        Node new_node = new Node(new_data);

        new_node.next = head;

        head = new_node;
    }

    void merge(LinkedList q)
    {
        Node p_curr = head, q_curr = q.head;
        Node p_next, q_next;

        while (p_curr != null && q_curr != null) {

            p_next = p_curr.next;
            q_next = q_curr.next;

            q_curr.next = p_next; 
            p_curr.next = q_curr; 

            p_curr = p_next;
            q_curr = q_next;
        }
        q.head = q_curr;
    }

    void printList()
    {
        Node temp = head;
        while (temp != null)
        {
           System.out.print(temp.data+" ");
           temp = temp.next;
        }
        System.out.println();
    }

    public static void main(String args[])
    {
        LinkedList llist1 = new LinkedList();
        LinkedList llist2 = new LinkedList();
        llist1.push(18);
        llist1.push(17);
        llist1.push(7);
        llist1.push(8);
 
        System.out.println("Linked List A: ");
        llist1.printList();
 
        llist2.push(4);
        llist2.push(2);
        llist2.push(10);
        llist2.push(32);
 
        System.out.println("Linked List B: ");

        System.out.println("Merging List B into List A at alternate positions in A");
 
        llist1.merge(llist2);
 
        System.out.println("Output Linked List A: ");
        llist1.printList();
 
        System.out.println("Output Linked List B: ");
        llist2.printList();
    }
}

class Node(object):
    def __init__(self, data:int):
        self.data = data
        self.next = None


class LinkedList(object):
    def __init__(self):
        self.head = None
        
    def push(self, new_data:int):
        new_node = Node(new_data)
        new_node.next = self.head
        self.head = new_node
        
    def printList(self):
        temp = self.head
        while temp != None:
            print(temp.data,end=" ")
            temp = temp.next
            
    def merge(self, p, q):
        p_curr = p.head
        q_curr = q.head

        while p_curr != None and q_curr != None:

            p_next = p_curr.next
            q_next = q_curr.next
            q_curr.next = p_next 
            p_curr.next = q_curr 
            p_curr = p_next
            q_curr = q_next
            q.head = q_curr



llist1 = LinkedList()
llist2 = LinkedList()

llist1.push(18)
llist1.push(17)
llist1.push(7)
llist1.push(8)

llist2.push(4)
llist2.push(2)
llist2.push(10)
llist2.push(32)
print("First Linked List:")
llist1.printList()

print("\nSecond Linked List:")
llist2.printList()

llist1.merge(p=llist1, q=llist2)

print("\nModified first linked list:")
llist1.printList()

print("\nModified second linked list:")
llist2.printList()

Output

Linked List A: 5 ->7 ->17 ->13

Linked List B: 12 ->10 ->2 ->4

Merging List B into List A at alternate positions in A

Output Linked List A: 5 ->12 ->7 ->10 ->17 ->2 ->13 ->4

Output Linked List B: Empty linked list

Space Complexity merge two linked list alternatively: O(1), as only temporary variables are being created.

Conclusion
In conclusion, merging a linked list into another linked list at alternate positions offers a powerful technique to optimize memory usage and streamline code efficiency. Throughout this article, we have explored the intricacies of merging, its applications, and various algorithms that enable seamless integration. By leveraging this technique, developers can significantly enhance the performance of their algorithms and improve the overall user experience.

FAQs related to merge two linked list alternatively

Here are a few FAQs related to merge a linked list into another linked list at alternate positions.

Q1. What is merging a linked list at alternate positions?
Merging a linked list at alternate positions refers to the process of combining two linked lists by interweaving their elements in a specific manner. Instead of appending one list to the other, this technique interleaves the elements of both lists, creating a merged list with elements from the source lists arranged in an alternating pattern.

Q2. When should I use merging at alternate positions?
This merging technique proves beneficial in scenarios where developers aim to optimize memory usage and reduce redundancy. It finds application in various algorithms, particularly when working with large datasets or when conserving space is critical.

Q3. What are the advantages of merging linked lists at alternate positions?
By merging linked lists at alternate positions, developers can achieve better space complexity and streamline the performance of their algorithms. This technique optimizes memory utilization, contributing to more efficient and elegant code solutions.

Q4. What are the different approaches for merging linked lists at alternate positions?
Several algorithms facilitate merging linked lists at alternate positions, including iterative methods, recursive methods, and utilizing extra data structures like arrays or hash maps. Each approach has its own time and space complexities, catering to diverse programming needs.

Q5. Can merging at alternate positions be used in real-world applications?
Absolutely! This technique finds practical application in a wide range of scenarios, such as merging sorted lists, user interface manipulation, and data processing tasks. It is particularly valuable when implementing algorithms that operate on multiple linked lists and require optimization for time and space efficiency.

Leave a Reply

Your email address will not be published. Required fields are marked *

Close

Related Post