Sliding Window

CONCEPTS USED:

Sliding Window Technique

DIFFICULTY LEVEL:

Medium

PROBLEM STATEMENT(SIMPLIFIED):

Given an array A, we need to find two sub-arrays with specific lengths L and R such that sum of these sub-arrays is Maximum among all possible choices of sub-arrays and these sub-arrays don’t overlap each other.

NOTE:

1. Both sub-arrays should be continuous and should not contain same element.

2. Sub-array L can come after or before sub-array R.

For Example:

Input : A = [6, 3, 5, 2, 6, 8, 9] 
        L = 3, R = 2

Output : 32

Explanation: There can be many possible sub-arrays -

[6, 3, 5] [2, 6]
[6, 3, 5] [6, 8]
[6, 3, 5] [8, 9]

[3, 5, 2] [6, 8]
[3, 5, 2] [8, 9]

[5, 2, 6] [6, 3]
[5, 2, 6] [8, 9]

[2, 6, 8] [6, 3]
[2, 6, 8] [3, 5]

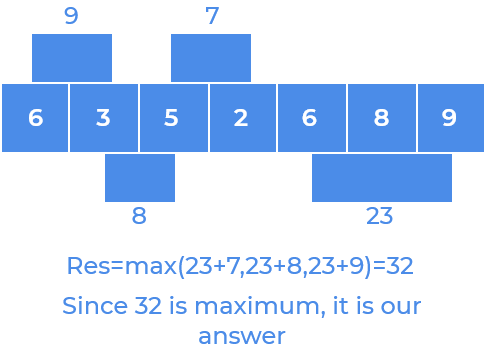
[6, 8, 9] [6, 3] --> It gives us maximum value = 32
[6, 8, 9] [3, 5]
[6, 8, 9] [5, 2]

SOLVING APPROACH:

BRUTE FORCE METHOD:

1. The simple solution would be to first traverse a sub-array for L elements and look for another sub-array with R elements from the remaining elements in the array ,take out their Sum and compare it with the initial max value.

2. Repeat this process for all such sub-arrays with length L and R and return the maximum possible value found.

3. Time Complexity of this solution will be O(N^2).

EXAMPLE:
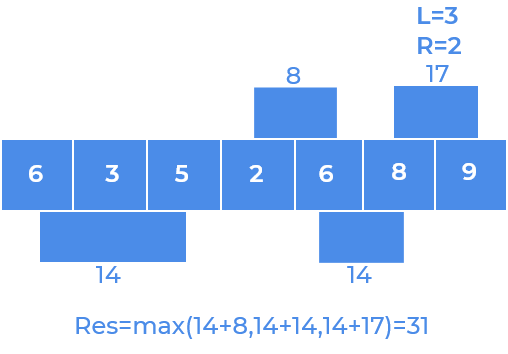
Step 1

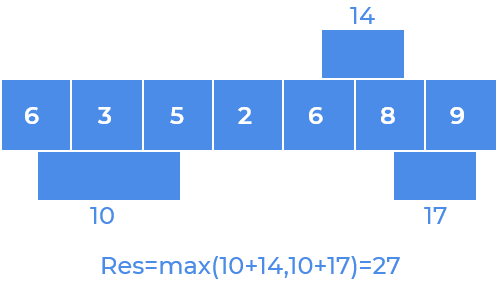
Step 2

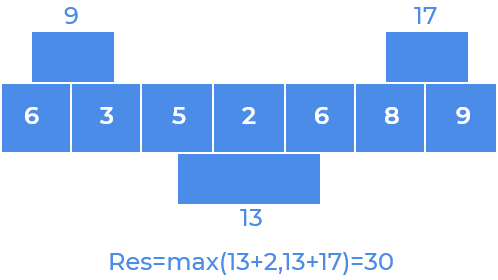
Step 3

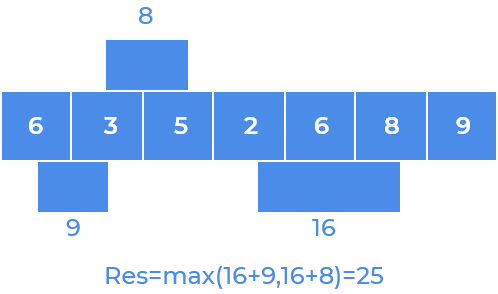
Step 4

Step 5

EFFICIENT METHOD:

1. The idea is to use Sliding Window Technique, where we create a window of (L+R) elements initially and keep processing all such windows present in the array.

2. Assume initialize variables Result as sum of first window of size (L+R), lmax as sum of first L elements and rmax as sum of first R elements.

3. Now move to the next window, we have two cases :

   • L comes before R.
   • R comes before L.

4. When L comes before R, we will find the sum of starting L elements of the current window as current left and compare it with our lmax value, the higher of the two will be stored in lmax, similarly calculate the sum of R elements as current right, and compare the current lmax + current right with Result and store the maximum of two in the Result.

5. When R comes before L, we will find the sum of starting R elements of the current window as current right and compare it with our rmax value, the higher of the two will be stored in rmax, similarly calculate the sum of L elements as current left, and compare the current rmax + current left with Result and store the maximum of two in the Result.

6. Similarly all such windows are processed from i= (left+right) to i<N.

NOTE: For finding the sum of ranges of array elements quickly, Prefix Sum Array can be used, which gives us the sum of any range of elements in an array in O(1) Time Complexity.

Illustration of Prefix Sum Array:

    A[]  = [1, 2, 3, 4, 5]
Prefix[] = [1, 3, 6, 10, 15]

where Prefix[index] gives us the sum of array till i = index.
    Prefix[3] = 10
Sum of elements in range [left, right] = Prefix[right] - Prefix[left-1]
                            sum [2, 4] = Prefix[4] - Prefix[2-1]
                                       = 15 - 3
                                       = 12

SOLUTIONS

#include <stdio.h>

int max(int a, int b){
  return (a>b) ? a:b;
}

int maxSumTwoNoOverlap(int *arr, int n, int l, int r){
  /* creating prefix sum array from existing array */
  for(int i=1; i<n; i++)
    arr[i] += arr[i-1];
  
  //initialize current values
  int res = arr[l+r-1];
  int lmax = arr[l-1];
  int rmax = arr[r-1];
  
  /* Running loop for traversing all the windows and 
    taking max values of left right and result */
  for(int i = l+r; i<n; i++){
    
    lmax = max(lmax, arr[i-r] - arr[i-r-l]);
    res = max(res, arr[i] - arr[i-r] + lmax);
    
    rmax = max(rmax, arr[i-l] - arr[i-r-l]);
    res = max(res, arr[i] - arr[i-l] + rmax);
  }
  return res;
}

int main()
{
  int t; scanf("%d", &t);
  while(t--){
    int n; scanf("%d", &n);
    int arr[n]; 
    for(int i=0; i<n; i++)
      scanf("%d", &arr[i]);
    int l, r; scanf("%d %d", &l , &r);
    
    printf("%d\n", maxSumTwoNoOverlap(arr, n, l, r));
  }
  return 0;
}

#include <bits/stdc++.h>
using namespace std;

int maxSumTwoNoOverlap(int *arr, int n, int l, int r){
  /* creating prefix sum array from existing array */
  for(int i=1; i<n; i++)
    arr[i] += arr[i-1];
  
  //initialize current values
  int res = arr[l+r-1];
  int lmax = arr[l-1];
  int rmax = arr[r-1];
  
  /* Running loop for traversing all the windows and 
    taking max values of left right and result */
  for(int i = l+r; i<n; i++){
    
    lmax = max(lmax, arr[i-r] - arr[i-r-l]);
    res = max(res, arr[i] - arr[i-r] + lmax);
    
    rmax = max(rmax, arr[i-l] - arr[i-r-l]);
    res = max(res, arr[i] - arr[i-l] + rmax);
  }
  return res;
}

int main()
{
  int t; cin>>t;
  while(t--){
    int n; cin>>n;
    int arr[n]; 
    for(int i=0; i<n; i++)
      cin>>arr[i];
    int l, r; cin>>l>>r;
    
    cout<<maxSumTwoNoOverlap(arr, n, l, r)<<"\n";
    
  }
  
  return 0;
}

import java.util.*;
import java.io.*;
import java.lang.Math;

public class Main {
  static int maxSumTwoNoOverlap(int []arr, int n, int l, int r){
    
  /* creating prefix sum array from existing array */
  for(int i=1; i<n; i++)
    arr[i] += arr[i-1];
  
  //initialize current values
  int res = arr[l+r-1];
  int lmax = arr[l-1];
  int rmax = arr[r-1];
  
  /* Running loop for traversing all the windows and 
    taking max values of left right and result */
  for(int i = l+r; i<n; i++){
    
    lmax = Math.max(lmax, arr[i-r] - arr[i-r-l]);
    res = Math.max(res, arr[i] - arr[i-r] + lmax);
    
    rmax = Math.max(rmax, arr[i-l] - arr[i-r-l]);
    res = Math.max(res, arr[i] - arr[i-l] + rmax);
  }
  return res;
}
  public static void main(String args[]) throws IOException {
    
    Scanner sc = new Scanner(System.in);
    int t = sc.nextInt();
    while(t != 0){
      int n = sc.nextInt();
      int arr[] = new int[n]; 
      for(int i=0; i<n; i++)
        arr[i] = sc.nextInt();
      int l = sc.nextInt();
      int r = sc.nextInt();
      
      System.out.println(maxSumTwoNoOverlap(arr, n, l, r));
      t--;
    }
  }
}

[forminator_quiz id="285"]

This article tried to discuss Sliding Window Technique. Hope this blog helps you understand and solve the problem. To practice more problems on Sliding Window Technique you can check out .