Get free ebooK with 50 must do coding Question for Product Based Companies solved
Fill the details & get ebook over email
Thank You!
We have sent the Ebook on 50 Must Do Coding Questions for Product Based Companies Solved over your email. All the best!
Graphs Interview Questions

Number of islands

Prepbytes

Concepts Used

Depth First Search, Disjoint Set

Difficulty Level

Medium

Problem Statement :

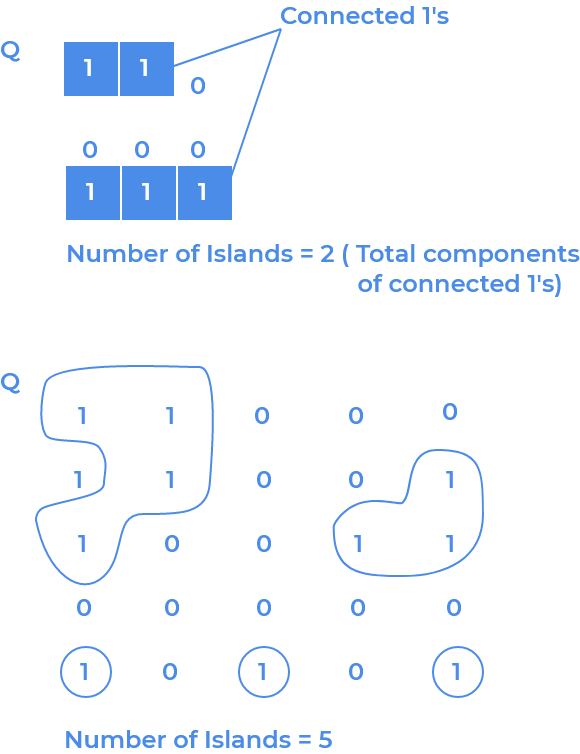
Given a 2D matrix, which contains only two numbers 0 or 1. In the map group of connected 0 represents, the water and group of connected 1 represent the island. Find the number of islands.

Solution Approach :

Introduction :

A group of connected 1’s represents an island.
Idea is to consider the 1’s and look for their neightbours if they form a component together it will be counted as 1 island.

This problem can be solved by many ways like Breadth First Search, Depth First Search or Disjoint Set. Below we are going to discuss two of the above mentioned methods to solve this problem.

EXAMPLE:

Method 1 (Using DFS) :

In this method we are going to use Depth First Search or DFS to find total number of connected components. In dfs(), we are going to traverse all the adjacent vertices(cells) which are not yet visited and mark them as visited so we won’t traverse them again. Once we encounter a cell which has value 1, then we will look for all its neighbour cells for the 1's by calling dfs() and count them as a single component, then increment count by 1.
We can keep track if the node is visited or not, using a boolean visited[ ] array of size n which is initially set false (why ?).

Now the question arise, why are we counting the different calls made to dfs() ? The answer lies in the fact that each time we call our dfs() function with some vertex v, it marks all vertices(cells) which are connected to v as visited, which means the we are visiting the vertices which are directly or indirectly connected to the v and has value 1. This is considered as one island. So each call made up to dfs() with some unvisited vertex v, gives us the different connected islands.

Method 2 (Using Disjoint Set) :

Disjoint Set Union or DSU data structure is also sometimes called Union-Find Set. This data structure is used to keep track of the different disjoint sets.
It basically performs two operations :

  1. Union : It takes two vertices and join them in a single set (if it is not already there).
  2. Find : Determines in which subset the element is.

We will use a parent[] array to keep track of the parents of each vertex. ith element will store the root/parent of ith vertex. Now, iterate through each cell or vertex of the matrix, if any cell has 1 then we will look for its neighbours if it has a value 1. If we find any such neighbour we will perform union() for the cell and its neighbour (both having 1) and update the parent[] array.
Now, iterate each value of the matrix again, this time if we will find 1, we will look for its root (or its set).
Now, iterate for all elements of matrix again, for each vertex/cell c, we will find root of c using find() and keep track of all distinct roots. Every time we encounter a distinct root increment the counter by 1.

Each disjoint set stores the vertices which are connected (directly or indirectly) to each other and has no relation/connection with any other vertex (as it is non overlapping set), which means each set itself represents a connected islands and since each set contains exactly one vertex as its root, the sum of distinct roots of all sets gives us the total number of connected islands.

Algorithms :

dfs() :

  1. For each call, for some vertex v ( dfs(v) ), we will mark the vertex v as visited (visited[v]= true).
  2. Iterate for all the adjacent vertices of v and for every adjacent vertex a, do following :
    • if a is not visited i.e visited[a]= false,
      and if a has value 1.
    • recursively call dfs (a).

union() :

  1. For two vertices u & v, find the root for both vertices using find() (a=find(u) & b = find(v)).
  2. If the root of u & v are not similar, check the level of a & b as follows:
    • if (level[a]>* else if (level[a]>level[b]), update parent[b] = a`.
    • else , update parent[b]=a & update level[a] = level[a]+1

find() :

  1. If (parent[v]==v), returns the vertex v (which is root).
  2. Else, update parent[v] by recursively looking up the tree for the root. (find(parent[v])).

Complexity Analysis:

The time complexity of the first method is represented in the form of O(R*C), where R is the number of rows and c is the number of columns.

Talking about method 2 using Union-Find data structure, since we have used path compression & union by rank (refer to Disjoint Set article for more detailed explanation), we will reach nearly constant time O(1) for each query. But we are traversing the matrix which gives us the time complexity O(R*C) for this method as well.

Solutions:


#include <stdbool.h> 
    #include <stdio.h> 
    #include <string.h> 

    int ROW,COL;


    int isSafe(int M[][COL], int row, int col, bool visited[][COL]) 
    { 
        return (row >= 0) && (row < ROW) && (col >= 0) && (col < COL) && (M[row][col] && !visited[row][col]); 
    } 

    void DFS(int M[][COL], int row, int col, bool visited[][COL]) 
    { 

        static int rowNbr[] = { -1, -1, -1, 0, 0, 1, 1, 1 }; 
        static int colNbr[] = { -1, 0, 1, -1, 1, -1, 0, 1 }; 

        // Mark this cell as visited 
        visited[row][col] = true; 

        // Recur for all connected neighbours 
        for (int k = 0; k < 8; ++k) 
            if (isSafe(M, row + rowNbr[k], col + colNbr[k], visited)) 
                DFS(M, row + rowNbr[k], col + colNbr[k], visited); 
    } 

    int countIslands(int M[][COL]) 
    { 

        bool visited[ROW][COL]; 
        memset(visited, 0, sizeof(visited)); 

        int count = 0; 
        for (int i = 0; i < ROW; ++i) 
            for (int j = 0; j < COL; ++j) 
                if (M[i][j] && !visited[i][j]) 
                { 
                    DFS(M, i, j, visited); 
                    ++count;  
                } 

        return count; 
    } 


    int main() 
    { 
    int t;
    scanf("%d",&t);
    while(t--)
    {
    scanf("%d %d",&ROW,&COL);
        int M[ROW][COL];
        for(int i=0;i<ROW;i++)
        {
        for(int j=0;j<COL;j++)
        {
            scanf("%d",&M[i][j]);
        }
        }

        printf("%d\n", countIslands(M)); 
    }

        return 0; 
    } 


#include <bits/stdc++.h> 
    using namespace std; 

    class  DisjointUnionSets 
    { 

    vector<int> rank, parent; 
    int n; 

    public: 
    DisjointUnionSets(int n) 
    { 
        rank.resize(n); 
        parent.resize(n); 
        this->n = n; 
        makeSet(); 
    } 

    void makeSet() 
    { 
        for(int i = 0; i < n; i++) 
            parent[i] = i; 
    } 

        int find(int x) 
        { 
            if(parent[x] != x) 
            { 

                return parent[x] = find(parent[x]); 
            } 

        return x; 
    } 

        void Union(int x, int y) 
        { 
            int xRoot = find(x); 
            int yRoot = find(y); 

            if(xRoot == yRoot) 
                    return; 

            if(rank[xRoot] < rank[yRoot]) 
                    parent[xRoot] = yRoot; 

            else if (rank[yRoot] < rank[xRoot]) 
                    parent[yRoot] = xRoot; 

            else     
            { 
                    parent[yRoot] = xRoot; 

                    // And increment the result tree's 
                    // rank by 1 
                    rank[xRoot] = rank[xRoot] + 1; 
            } 
        } 
    }; 

    int countIslands(vector<vector<int>> a,int n,int m) 
    { 


        DisjointUnionSets *dus = new DisjointUnionSets(n * m); 

        for(int j = 0; j < n; j++) 
        { 
            for(int k = 0; k < m; k++) 
            { 
                    // If cell is 0, nothing to do 
                    if (a[j][k] == 0) 
                    continue; 

                    // Check all 8 neighbours and do a Union 
                    // with neighbour's set if neighbour is 
                    // also 1 
                    if (j + 1 < n && a[j + 1][k] == 1) 
                    dus->Union(j * (m) + k,(j + 1) * (m) + k); 
                    if (j - 1 >= 0 && a[j - 1][k] == 1) 
                    dus->Union(j * (m) + k, 
                        (j - 1) * (m) + k); 
                    if (k + 1 < m && a[j][k + 1] == 1) 
                    dus->Union(j * (m) + k, 
                        (j) * (m) + k + 1); 
                    if (k - 1 >= 0 && a[j][k - 1] == 1) 
                    dus->Union(j * (m) + k, 
                        (j) * (m) + k - 1); 
                    if (j + 1 < n && k + 1 < m && 
                    a[j + 1][k + 1] == 1) 
                    dus->Union(j * (m) + k, 
                        (j + 1) * (m) + k + 1); 
                    if (j + 1 < n && k - 1 >= 0 && 
                    a[j + 1][k - 1] == 1) 
                    dus->Union(j * m + k, 
                        (j + 1) * (m) + k - 1); 
                    if (j - 1 >= 0 && k + 1 < m && 
                    a[j - 1][k + 1] == 1) 
                    dus->Union(j * m + k, 
                        (j - 1) * m + k + 1); 
                    if (j - 1 >= 0 && k - 1 >= 0 && 
                    a[j - 1][k - 1] == 1) 
                    dus->Union(j * m + k, 
                        (j - 1) * m + k - 1); 
        } 
    } 


    set<int> s;
    for(int j = 0; j < n; j++) 
        { 
        for(int k = 0; k < m; k++) 
            { 

                if (a[j][k] == 1) 
                 s.insert(dus->find(j * m + k));
            } 
        } 
        return s.size(); 
    } 

        int main(void) 
        { 
            int t;
            cin>>t;
            while(t--)
            {
                 int r,c;
                 cin>>r>>c;
                 vector<vector<int>> a(r);
                 for(int i=0;i<r;i++)
                 {
                 for(int j=0;j<c;j++)
                 {
                 int t;
                 cin>>t;
                 a[i].push_back(t);
                 }
                 }

                 cout<< countIslands(a,r,c) << endl; 
            }
        } 


 import java.io.*; 
    import java.util.*; 

    public class Main 
    { 
    public static void main(String[] args)throws IOException 
    { 
      Scanner sc = new Scanner(System.in);
      int t = sc.nextInt();
      while(t-->0)
      {
       int r = sc.nextInt();
       int c = sc.nextInt();
       int [][]a = new int[r][c];

       for(int i =0;i<r;i++)
       {
         for(int j=0;j<c;j++)
         {
           a[i][j] = sc.nextInt();
         }
       }

       System.out.println(countIslands(a)); 
      }
    } 

    // Returns number of islands in a[][] 
    static int countIslands(int a[][]) 
    { 
        int n = a.length; 
        int m = a[0].length; 

        DisjointUnionSets dus = new DisjointUnionSets(n*m); 

        /* The following loop checks for its neighbours 
        and unites the indexes if both are 1. */
        for (int j=0; j<n; j++) 
        { 
            for (int k=0; k<m; k++) 
            { 
                // If cell is 0, nothing to do 
                if (a[j][k] == 0) 
                    continue; 

                // Check all 8 neighbours and do a union 
                // with neighbour's set if neighbour is 
                // also 1 
                if (j+1 < n && a[j+1][k]==1) 
                    dus.union(j*(m)+k, (j+1)*(m)+k); 
                if (j-1 >= 0 && a[j-1][k]==1) 
                    dus.union(j*(m)+k, (j-1)*(m)+k); 
                if (k+1 < m && a[j][k+1]==1) 
                    dus.union(j*(m)+k, (j)*(m)+k+1); 
                if (k-1 >= 0 && a[j][k-1]==1) 
                    dus.union(j*(m)+k, (j)*(m)+k-1); 
                if (j+1<n && k+1<m && a[j+1][k+1]==1) 
                    dus.union(j*(m)+k, (j+1)*(m)+k+1); 
                if (j+1<n && k-1>=0 && a[j+1][k-1]==1) 
                    dus.union(j*m+k, (j+1)*(m)+k-1); 
                if (j-1>=0 && k+1<m && a[j-1][k+1]==1) 
                    dus.union(j*m+k, (j-1)*m+k+1); 
                if (j-1>=0 && k-1>=0 && a[j-1][k-1]==1) 
                    dus.union(j*m+k, (j-1)*m+k-1); 
            } 
        } 

        // Array to note down frequency of each set 
        int[] c = new int[n*m]; 
        int numberOfIslands = 0; 
        for (int j=0; j<n; j++) 
        { 
            for (int k=0; k<m; k++) 
            { 
                if (a[j][k]==1) 
                { 

                    int x = dus.find(j*m+k); 

                    // If frequency of set is 0, 
                    // increment numberOfIslands 
                    if (c[x]==0) 
                    { 
                        numberOfIslands++; 
                        c[x]++; 
                    } 

                    else
                        c[x]++; 
                } 
            } 
        } 
        return numberOfIslands; 
     } 
    } 


    class DisjointUnionSets 
    { 
    int[] rank, parent; 
    int n; 

    public DisjointUnionSets(int n) 
    { 
        rank = new int[n]; 
        parent = new int[n]; 
        this.n = n; 
        makeSet(); 
    } 

    void makeSet() 
    { 
        // Initially, all elements are in their 
        // own set. 
        for (int i=0; i<n; i++) 
            parent[i] = i; 
    } 

    int find(int x) 
    { 
        if (parent[x] != x) 
        { 
            return parent[x] = find(parent[x]); 
        } 

        return x; 
    } 

    void union(int x, int y) 
    { 
        int xRoot = find(x); 
        int yRoot = find(y); 
        if (xRoot == yRoot) 
            return; 

        if (rank[xRoot] < rank[yRoot]) 
            parent[xRoot] = yRoot; 

        else if(rank[yRoot]<rank[xRoot]) 
            parent[yRoot] = xRoot; 

        else 
        { 
            parent[yRoot] = xRoot; 
            rank[xRoot] = rank[xRoot] + 1; 
        } 
      } 
    }

[forminator_quiz id="2121"]

So, in this blog, we have tried to explain the concept of Depth First Search, Disjoint Set. If you want to solve more questions on Graphs, which are curated by our expert mentors at PrepBytes, you can follow this link Graphs.

Leave a Reply

Close

Related Post